Cómo utilizar el método de mínimos cuadrados en Excel
En el mundo del análisis de datos, encontrar la relación entre variables puede ser un desafío apasionante. Si alguna vez te has preguntado cómo transformar un conjunto de datos en insights valiosos, el método de mínimos cuadrados se presenta como una herramienta indispensable. Este enfoque matemático no solo te permite ajustar una línea a tus puntos de datos, sino que también te ayuda a predecir tendencias futuras con sorprendente precisión. En este artículo, te mostraremos paso a paso cómo aplicar este poderoso método en Excel, ¡y convertir tus hojas de cálculo en verdaderos laboratorios de análisis! Prepárate para desatar todo el potencial de tus datos y llevar tu toma de decisiones al siguiente nivel.
El método de mínimos cuadrados es una herramienta matemática esencial para analizar y entender los datos en un conjunto de información. A través de este método, es posible determinar la relación entre variables y predecir valores desconocidos con mayor precisión. En este artículo, aprenderemos cómo utilizar el método de mínimos cuadrados en Excel, una de las herramientas más utilizadas en el mundo empresarial y académico. Descubre cómo sacar el máximo provecho de Excel para obtener resultados eficientes y confiables en tus análisis estadísticos. ¡Sigue leyendo para conocer todos los detalles!
El método de mínimos cuadrados es un método que podemos utilizar para encontrar la línea de regresión que mejor se ajuste a un conjunto de datos determinado.
El siguiente vídeo proporciona una breve explicación de este método:
Para utilizar el método de mínimos cuadrados para ajustar una recta de regresión en Excel, podemos utilizar el =ESTIMACIÓN LINEAL() función.
El siguiente ejemplo muestra paso a paso cómo utilizar esta función en la práctica.
Paso 1: crear el conjunto de datos
Primero, creemos el siguiente conjunto de datos en Excel:

>Paso 2: utilice el método de mínimos cuadrados para ajustar la línea de regresión
Podemos usar el = ESTIMACIÓN LINEAL (ys_conocido, xs_conocido) función para utilizar el método de mínimos cuadrados para ajustar una línea de regresión a este conjunto de datos:
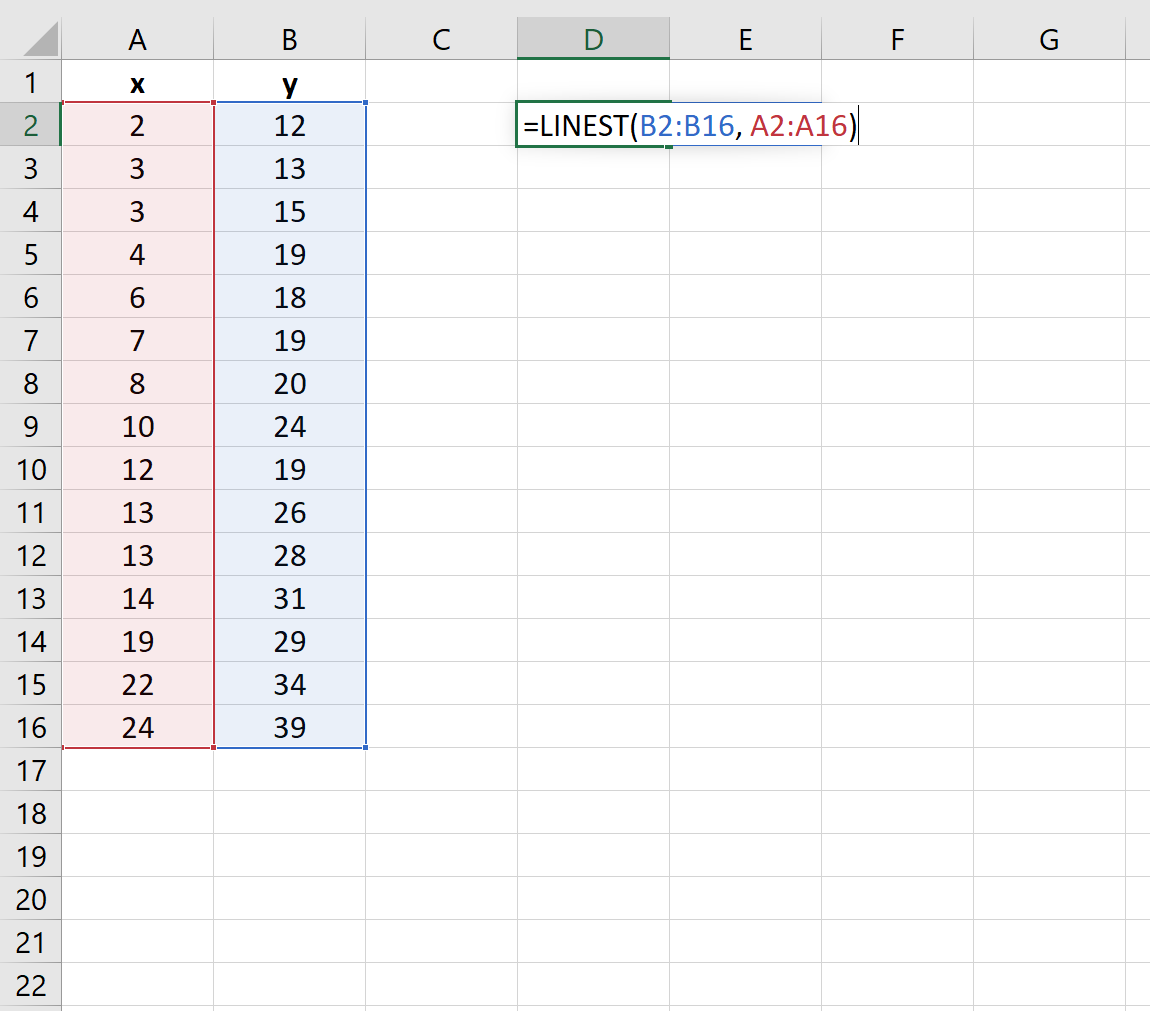
>Una vez que presionamos INGRESARaparecerán los coeficientes del modelo de regresión:
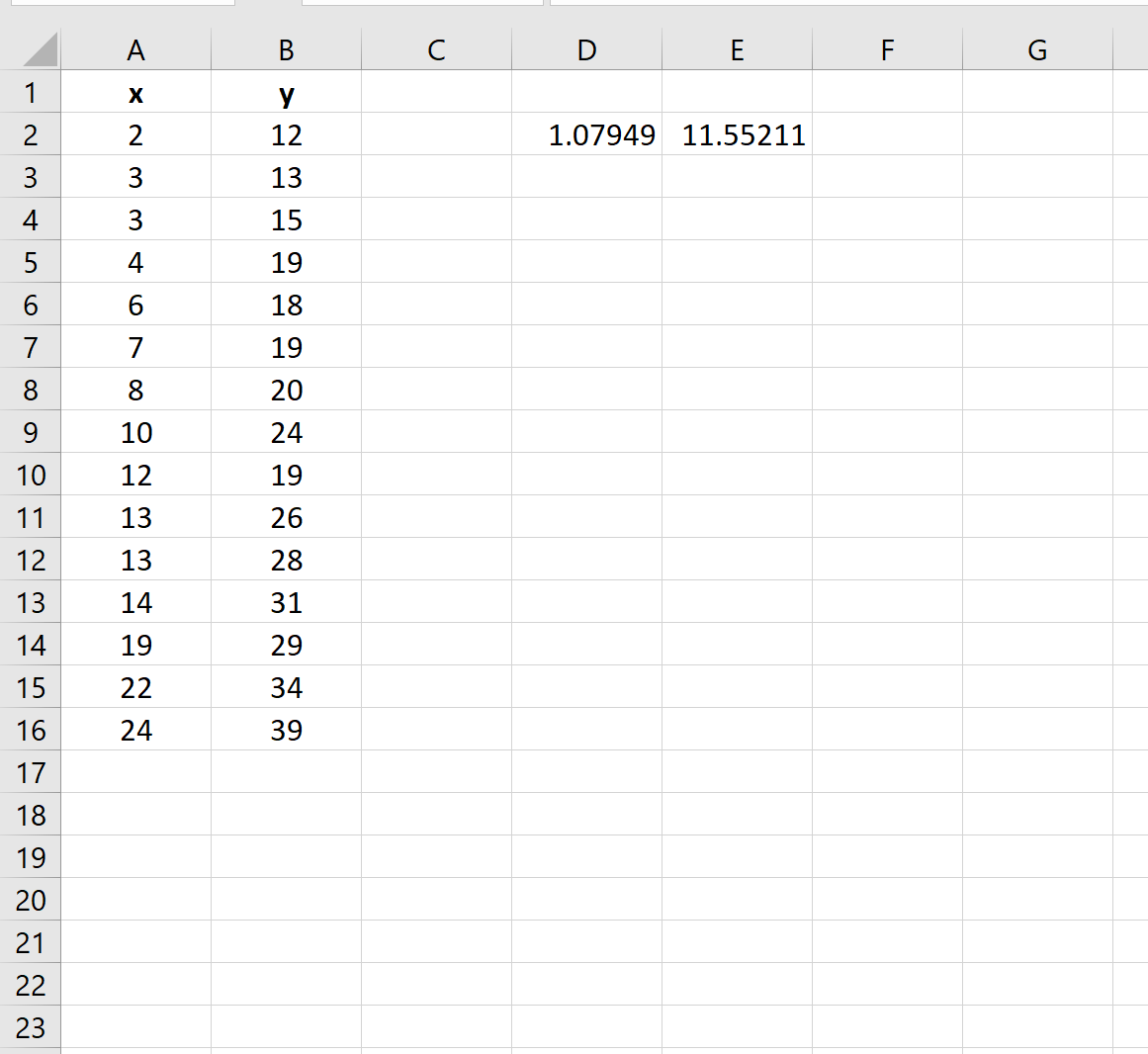
>Paso 3: interpretar los resultados
Usando los coeficientes de la =ESTIMACIÓN LINEAL() función, podemos escribir la siguiente línea de regresión ajustada:
y = 11,55211 + 1,07949(x)
Podemos usar esta ecuación para estimar el valor de y en función del valor de x.
Por ejemplo, si x = 10 entonces estimaríamos que y sería igual a 22.347:
y = 11,55211 + 1,07949(10) = 22,347
Paso 4: trazar los resultados
Por último, podemos utilizar los siguientes pasos para trazar el conjunto de datos junto con la línea de regresión ajustada:
- Resaltar celdas A2:B16.
- Haga clic en el Insertar pestaña a lo largo de la cinta superior. Luego haga clic en la primera opción de gráfico titulada Insertar gráfico de dispersión (X, Y) o de burbujas en el grupo Gráficos.
- Una vez que aparezca el gráfico, haga clic en el signo más “+” en la esquina superior derecha. En el menú desplegable, haga clic en la casilla de verificación junto a Línea de tendencia para agregar la línea de regresión ajustada al gráfico.

>Recursos adicionales
Cómo realizar una regresión lineal múltiple en Excel
Cómo realizar una regresión cuadrática en Excel
Cómo realizar una regresión polinómica en Excel
Ajuste de curvas en Excel (con ejemplos)
Cómo utilizar el método de mínimos cuadrados en Excel – Preguntas frecuentes
Preguntas frecuentes sobre el método de mínimos cuadrados en Excel
¿Qué es el método de mínimos cuadrados?
El método de mínimos cuadrados es una técnica utilizada en estadística y ajuste de curvas para encontrar la línea que mejor se ajusta a un conjunto de puntos. En Excel, este método se utiliza para calcular la pendiente (m) e intercepto (b) de una línea de tendencia.
¿Cuál es la fórmula del método de mínimos cuadrados?
La fórmula para calcular la pendiente (m) e intercepto (b) de una línea de tendencia utilizando el método de mínimos cuadrados es:
m = (∑(xi – x̄)(yi – ȳ)) / ∑(xi – x̄)²
b = ȳ – m * x̄
donde xi y yi son las coordenadas de cada punto, x̄ es la media de los valores de x y ȳ es la media de los valores de y.
¿Cómo calcular el método de mínimos cuadrados en Excel?
Para calcular el método de mínimos cuadrados en Excel, debes seguir los siguientes pasos:
¿Dónde puedo obtener más información sobre el método de mínimos cuadrados en Excel?
Si deseas obtener más información detallada sobre cómo utilizar el método de mínimos cuadrados en Excel, te recomendamos visitar los siguientes recursos:
- Support de Microsoft – Ajustar un curve mediante la regresión polinómica en Excel
- Excel Total – Regresión Lineal en Excel
- Wikipedia – Regresión lineal
Recuerda que el método de mínimos cuadrados es una herramienta poderosa para analizar tendencias y realizar predicciones basadas en datos. ¡Practica y experimenta con diferentes conjuntos de datos para familiarizarte con su aplicación!
El método de mínimos cuadrados es un método que podemos utilizar para encontrar la línea de regresión que mejor se ajuste a un conjunto de datos determinado.
El siguiente vídeo proporciona una breve explicación de este método:
Para utilizar el método de mínimos cuadrados para ajustar una recta de regresión en Excel, podemos utilizar el =ESTIMACIÓN LINEAL() función.
El siguiente ejemplo muestra paso a paso cómo utilizar esta función en la práctica.
Paso 1: crear el conjunto de datos
Primero, creemos el siguiente conjunto de datos en Excel:

>Paso 2: utilice el método de mínimos cuadrados para ajustar la línea de regresión
Podemos usar el = ESTIMACIÓN LINEAL (ys_conocido, xs_conocido) función para utilizar el método de mínimos cuadrados para ajustar una línea de regresión a este conjunto de datos:

>Una vez que presionamos INGRESARaparecerán los coeficientes del modelo de regresión:

>Paso 3: interpretar los resultados
Usando los coeficientes de la =ESTIMACIÓN LINEAL() función, podemos escribir la siguiente línea de regresión ajustada:
y = 11,55211 + 1,07949(x)
Podemos usar esta ecuación para estimar el valor de y en función del valor de x.
Por ejemplo, si x = 10 entonces estimaríamos que y sería igual a 22.347:
y = 11,55211 + 1,07949(10) = 22,347
Paso 4: trazar los resultados
Por último, podemos utilizar los siguientes pasos para trazar el conjunto de datos junto con la línea de regresión ajustada:
- Resaltar celdas A2:B16.
- Haga clic en el Insertar pestaña a lo largo de la cinta superior. Luego haga clic en la primera opción de gráfico titulada Insertar gráfico de dispersión (X, Y) o de burbujas en el grupo Gráficos.
- Una vez que aparezca el gráfico, haga clic en el signo más “+” en la esquina superior derecha. En el menú desplegable, haga clic en la casilla de verificación junto a Línea de tendencia para agregar la línea de regresión ajustada al gráfico.

>Recursos adicionales
Cómo realizar una regresión lineal múltiple en Excel
Cómo realizar una regresión cuadrática en Excel
Cómo realizar una regresión polinómica en Excel
Ajuste de curvas en Excel (con ejemplos)
[automatic_youtube_gallery type=»search» search=»Cómo utilizar el método de mínimos cuadrados en Excel» limit=»1″]
Cómo utilizar el método de mínimos cuadrados en Excel
En el mundo del análisis de datos, encontrar la relación entre variables puede ser un desafío apasionante. Si alguna vez te has preguntado cómo transformar un conjunto de datos en insights valiosos, el método de mínimos cuadrados se presenta como una herramienta indispensable. Este enfoque matemático no solo te permite ajustar una línea a tus puntos de datos, sino que también te ayuda a predecir tendencias futuras con sorprendente precisión.
En este artículo, te mostraremos paso a paso cómo aplicar este poderoso método en Excel, ¡y convertir tus hojas de cálculo en verdaderos laboratorios de análisis! Prepárate para desatar todo el potencial de tus datos y llevar tu toma de decisiones al siguiente nivel.
¿Qué es el método de mínimos cuadrados?
El método de mínimos cuadrados es una técnica utilizada en estadística y ajuste de curvas para encontrar la línea que mejor se ajusta a un conjunto de puntos. Este método busca minimizar la suma de los cuadrados de las diferencias entre los valores observados y los valores esperados en una regresión lineal.
Cómo utilizar el método de mínimos cuadrados en Excel
Paso 1: Crear el conjunto de datos
Primero, crea un conjunto de datos en Excel. Por ejemplo, puedes tener dos columnas, una con valores de x y otra con valores de y.
Paso 2: Utilizar la función de estimación lineal
Para ajustar la línea de regresión, utiliza la función =ESTIMACIÓN.LINEAL(ys_conocidos, xs_conocidos). Esta función calculará los coeficientes del modelo de regresión. Presiona Enter y aparecerán los resultados.
Paso 3: Interpretar los resultados
Usando los coeficientes obtenidos de la función, puedes escribir la ecuación de la línea de regresión ajustada. Por ejemplo, si los coeficientes son m y b, tu ecuación será:
y = b + m * x
Esto te permitirá estimar el valor de y en función de x. Por ejemplo, si x = 10, puedes estimar el valor de y a partir de la ecuación ajustada.
Paso 4: Trazar los resultados
Para visualizar los resultados junto con la línea de regresión, sigue estos pasos:
- Resalta las celdas con tus datos.
- Haz clic en la pestaña Insertar.
- Selecciona Gráfico de dispersión en el grupo de gráficos.
- Una vez que el gráfico aparezca, selecciona el signo «+» en la esquina superior derecha y marca Línea de tendencia para agregarla al gráfico.
Recursos adicionales
- Soporte de Microsoft – Ajustar una curva mediante la regresión polinómica en Excel
- Excel Total – Regresión Lineal en Excel
- Wikipedia – Regresión lineal
Preguntas frecuentes sobre el método de mínimos cuadrados en Excel
¿Cuál es la fórmula del método de mínimos cuadrados?
La fórmula para calcular la pendiente (m) e intercepto (b) de una línea de tendencia utilizando el método de mínimos cuadrados es:
m = (∑(xi – x̄)(yi – ȳ)) / ∑(xi – x̄)²
b = ȳ – m * x̄
donde xi y yi son las coordenadas de cada punto, x̄ es la media de los valores de x y ȳ es la media de los valores de y.
¿Cómo calcular el método de mínimos cuadrados en Excel?
Para calcular el método de mínimos cuadrados en Excel, debes seguir estos pasos:
- Organiza tus datos en dos columnas: una para los valores de x y otra para y.
- Calcula la media de los valores de x y de y.
- Resta la media de x a cada valor de x y la media de y a cada valor de y.
- Multiplica los resultados obtenidos por cada par de valores de x y y.
- Suma todos los resultados anteriores.
- Calcula la suma de los cuadrados de las diferencias entre los valores de x y su media.
- Calcula la pendiente (m) dividiendo la suma de resultados entre la suma de cuadrados de las diferencias.
- Calcula el intercepto (b) restando la pendiente media de y multiplicada a la media de x.
¿Dónde puedo obtener más información sobre el método de mínimos cuadrados en Excel?
Para obtener información más detallada sobre el método de mínimos cuadrados en Excel, te recomendamos visitar los recursos mencionados anteriormente. Allí encontrarás ejemplos prácticos y explicaciones más claras que te ayudarán a profundizar en su uso.
El método de mínimos cuadrados es una herramienta poderosa para analizar tendencias y realizar predicciones basadas en datos. ¡Practica y experimenta con diferentes conjuntos de datos para familiarizarte con su aplicación!