¿Te has preguntado alguna vez cómo desentrañar las relaciones entre múltiples variables y obtener predicciones más precisas en tus proyectos de análisis de datos? La regresión lineal múltiple es una herramienta poderosa que te permitirá hacerlo, y lo mejor de todo es que puedes realizarla fácilmente utilizando Excel, uno de los programas más accesibles y utilizados en el ámbito empresarial y académico. En este artículo, te guiaremos paso a paso a través del proceso de realizar una regresión lineal múltiple en Excel, revelando tanto los conceptos fundamentales como las técnicas prácticas para que puedas aplicar este conocimiento en tus propios análisis. Prepárate para transformar tus datos y descubrir patrones ocultos que te ayudarán a tomar decisiones más informadas. ¡Comencemos!
La regresión lineal múltiple es una herramienta estadística poderosa que nos permite analizar la relación entre múltiples variables independientes y una variable dependiente. En este artículo, te mostraremos cómo realizar una regresión lineal múltiple en Excel, una popular herramienta de hojas de cálculo que probablemente ya estés familiarizado. Así que ponte cómodo, saca tu computadora y prepárate para descubrir cómo utilizar Excel para realizar este tipo de análisis estadístico. ¡Comencemos!
Regresión lineal múltiple es un método que podemos utilizar para comprender la relación entre dos o más variables explicativas y una variable de respuesta.
Este tutorial explica cómo realizar una regresión lineal múltiple en Excel.
Nota: Si solo tiene una variable explicativa, debería realizar una regresión lineal simple.
Ejemplo: regresión lineal múltiple en Excel
Supongamos que queremos saber si la cantidad de horas dedicadas a estudiar y la cantidad de exámenes de preparación realizados afectan la puntuación que recibe un estudiante en un determinado examen de ingreso a la universidad.
Para explorar esta relación, podemos realizar una regresión lineal múltiple usando horas estudiadas y exámenes de preparación tomados como variables explicativas y puntuación del examen como variable de respuesta.
Realice los siguientes pasos en Excel para realizar una regresión lineal múltiple.
Paso 1: Ingresa los datos.
Ingrese los siguientes datos para la cantidad de horas estudiadas, exámenes de preparación realizados y puntaje de examen recibido para 20 estudiantes:
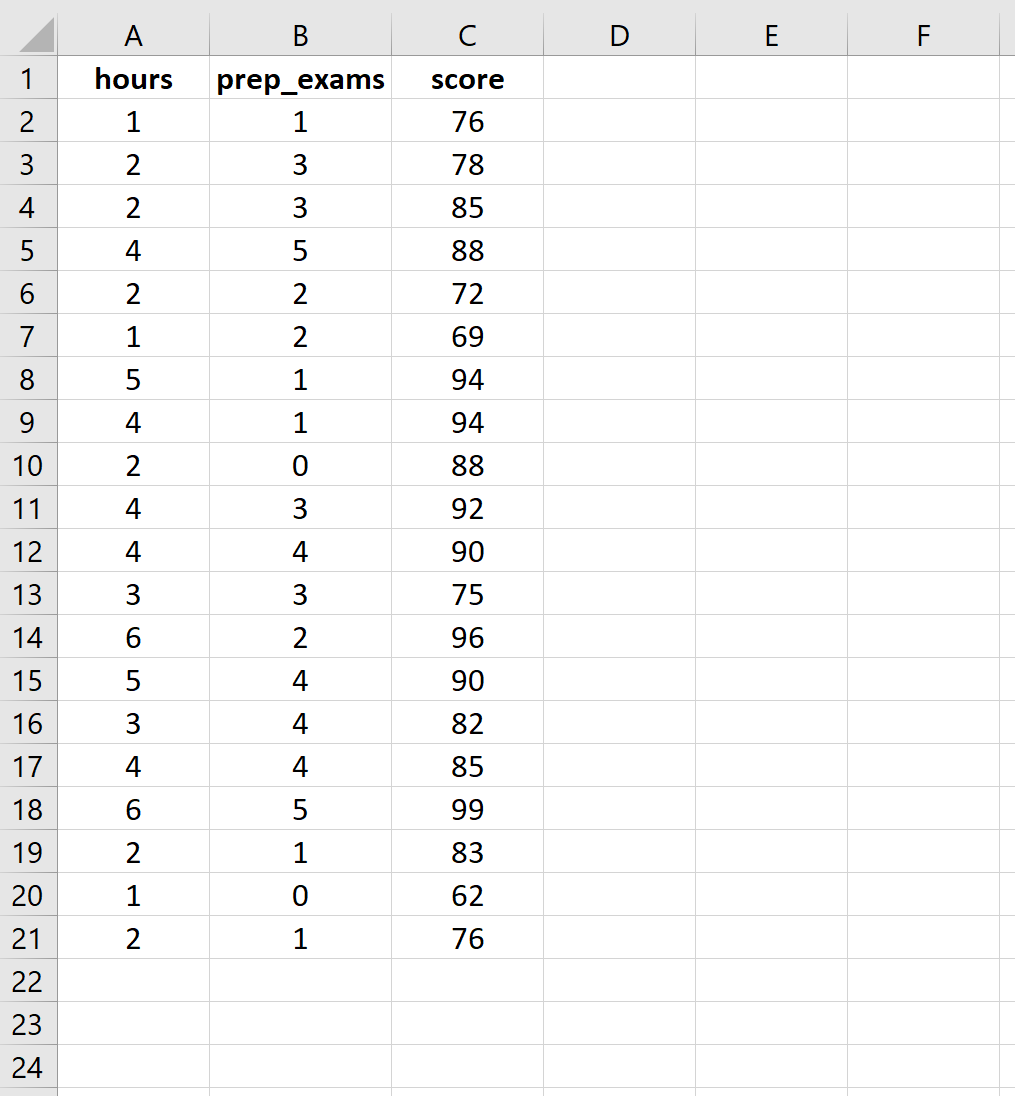
>Paso 2: realizar una regresión lineal múltiple.
A lo largo de la cinta superior en Excel, vaya a la Datos pestaña y haga clic en Análisis de los datos. Si no ve esta opción, primero debe Instale el paquete de herramientas de análisis gratuito.
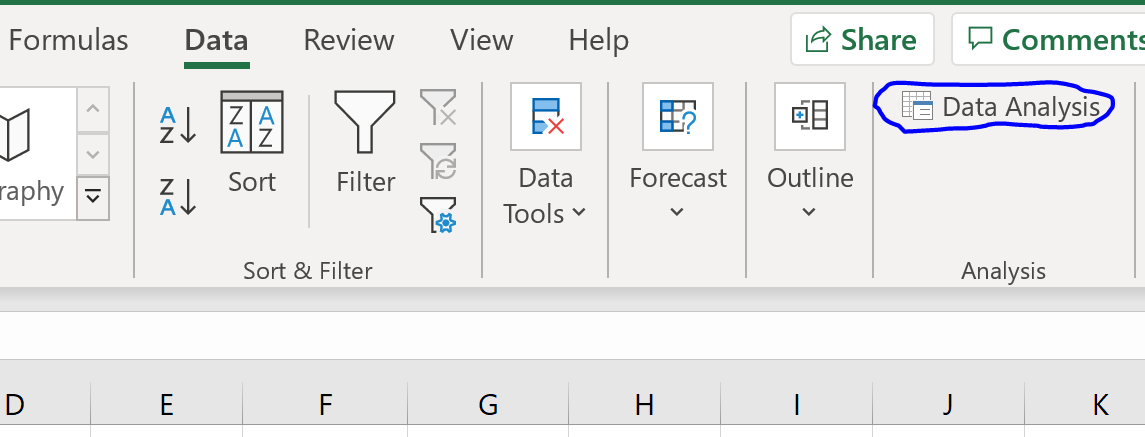
>Una vez que hagas clic en Análisis de los datos, Aparecerá una nueva ventana. Seleccionar Regresión y haga clic en Aceptar.

>Para Rango de entrada Y, complete la matriz de valores para la variable de respuesta. Para Rango de entrada X, complete la matriz de valores para las dos variables explicativas. Marque la casilla junto a Etiquetas entonces Excel sabe que incluimos los nombres de las variables en los rangos de entrada. Para Rango de salida, seleccione una celda donde desea que aparezca el resultado de la regresión. Luego haga clic DE ACUERDO.
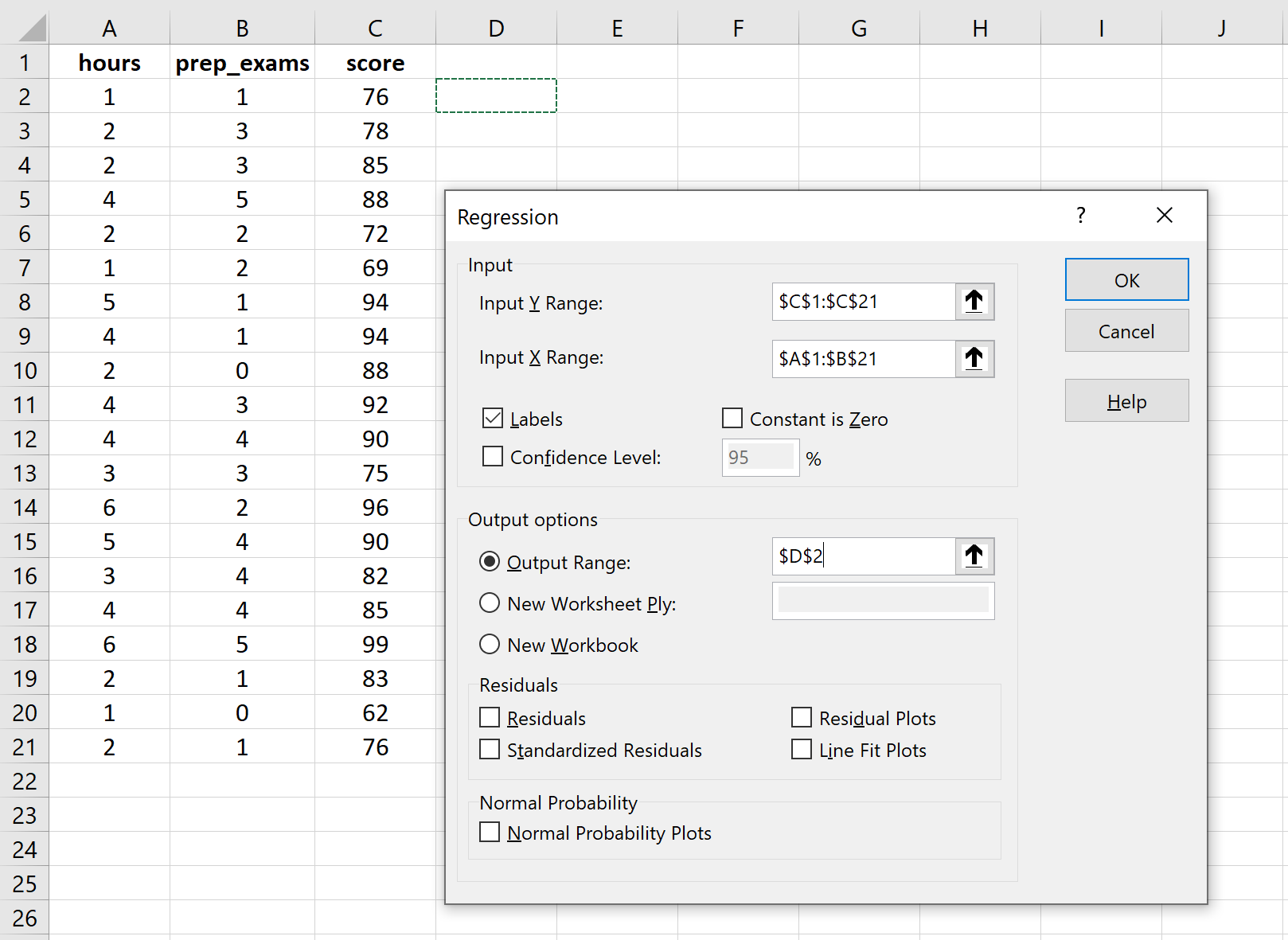
>Automáticamente aparecerá el siguiente resultado:

>Paso 3: interpretar el resultado.
A continuación se explica cómo interpretar los números más relevantes en el resultado:
R Plaza: 0.734. Esto se conoce como coeficiente de determinación. Es la proporción de la varianza en la variable de respuesta que puede explicarse por las variables explicativas. En este ejemplo, el 73,4% de la variación en las calificaciones de los exámenes se puede explicar por la cantidad de horas estudiadas y la cantidad de exámenes de preparación realizados.
Error estándar: 5.366. Esta es la distancia promedio a la que caen los valores observados desde la línea de regresión. En este ejemplo, los valores observados caen un promedio de 5,366 unidades desde la línea de regresión.
F: 23,46. Esta es la estadística F general para el modelo de regresión, calculada como MS de regresión/MS residual.
Significado F: 0,0000. Este es el valor p asociado con la estadística F general. Nos dice si el modelo de regresión en su conjunto es estadísticamente significativo o no. En otras palabras, nos dice si las dos variables explicativas combinadas tienen una asociación estadísticamente significativa con la variable de respuesta. En este caso el valor p es menor que 0,05, lo que indica que las variables explicativas horas estudiadas y exámenes de preparación tomados combinados tienen una asociación estadísticamente significativa con puntuación del examen.
Valores p. Los valores p individuales nos dicen si cada variable explicativa es estadísticamente significativa o no. Podemos ver eso horas estudiadas es estadísticamente significativo (p = 0,00) mientras que exámenes de preparación tomados (p = 0,52) no es estadísticamente significativo en α = 0,05. Desde exámenes de preparación tomados no es estadísticamente significativo, podemos terminar decidiendo eliminarlo del modelo.
Coeficientes: Los coeficientes de cada variable explicativa nos indican el cambio promedio esperado en la variable de respuesta, suponiendo que la otra variable explicativa permanece constante. Por ejemplo, por cada hora adicional dedicada a estudiar, se espera que la puntuación promedio del examen aumente en 5.56asumiendo que exámenes de preparación tomados permanece constante.
Aquí hay otra forma de pensar en esto: si el estudiante A y el estudiante B toman la misma cantidad de exámenes de preparación pero el estudiante A estudia una hora más, entonces se espera que el estudiante A obtenga una puntuación igual a 5.56 puntos más altos que el estudiante B.
Interpretamos que el coeficiente del intercepto significa que la puntuación esperada en el examen para un estudiante que estudia cero horas y no toma exámenes de preparación es 67,67.
Ecuación de regresión estimada: Podemos usar los coeficientes del resultado del modelo para crear la siguiente ecuación de regresión estimada:
puntuación del examen = 67,67 + 5,56*(horas) – 0,60*(exámenes de preparación)
Podemos usar esta ecuación de regresión estimada para calcular la puntuación esperada en el examen de un estudiante, en función de la cantidad de horas que estudia y la cantidad de exámenes de preparación que realiza. Por ejemplo, se espera que un estudiante que estudia durante tres horas y toma un examen de preparación reciba una puntuación de 83,75:
puntuación del examen = 67,67 + 5,56*(3) – 0,60*(1) = 83,75
Tenga en cuenta que porque exámenes de preparación tomados no fue estadísticamente significativo (p = 0,52), podemos decidir eliminarlo porque no agrega ninguna mejora al modelo general. En este caso, podríamos realizar una regresión lineal simple usando solo horas estudiadas como variable explicativa.
Los resultados de este análisis de regresión lineal simple se pueden encontrar aquí.
Recursos adicionales
Una vez que realice una regresión lineal múltiple, es posible que desee verificar varias suposiciones, entre ellas:
1. Pruebas de multicolinealidad mediante VIF.
2. Prueba de heterocedasticidad mediante la prueba de Breusch-Pagan.
3. Prueba de normalidad mediante un gráfico QQ.
Cómo realizar una regresión lineal múltiple en Excel
La regresión lineal múltiple es una técnica estadística que nos permite analizar la relación entre una variable dependiente y dos o más variables independientes. Esta herramienta es ampliamente utilizada en diversas disciplinas como la economía, la psicología y la ciencia de datos, entre otras.
Si estás interesado en realizar una regresión lineal múltiple en Excel, has llegado al lugar correcto. A continuación, te explicaremos paso a paso cómo llevar a cabo este análisis utilizando la popular hoja de cálculo de Microsoft.
Paso 1: Preparar los datos
Antes de iniciar el análisis de regresión, es fundamental contar con un conjunto de datos adecuado. Asegúrate de tener una columna para la variable dependiente y columnas separadas para cada una de las variables independientes. Además, los datos deben estar organizados en filas, donde cada fila representa una observación o muestra.
Recuerda que es recomendable tener al menos 30 observaciones para obtener resultados confiables en la regresión lineal múltiple.
Paso 2: Abrir Excel y seleccionar los datos
Una vez que tengas tus datos listos, abre Excel y crea un nuevo libro de trabajo. A continuación, selecciona la columna de la variable dependiente y las columnas de las variables independientes manteniendo presionada la tecla «Ctrl».
Adicionalmente, es importante asegurarse de que los datos seleccionados se encuentren en la misma hoja de cálculo.
Paso 3: Acceder a la herramienta de Análisis de Datos
Excel ofrece una gama de herramientas de análisis que pueden ser de gran utilidad en este proceso. Para acceder a estas herramientas, haz clic en la pestaña «Datos» en la parte superior de la hoja de cálculo y luego selecciona «Análisis de Datos» en el grupo «Análisis».
En caso de que la opción «Análisis de Datos» no aparezca, deberás habilitarla siguiendo los pasos indicados en este enlace.
Paso 4: Seleccionar «Regresión»
En el cuadro de diálogo «Análisis de Datos», busca y selecciona la opción «Regresión» y luego haz clic en «Aceptar».
Paso 5: Configurar las opciones de la regresión
En el cuadro de diálogo «Regresión», deberás configurar las opciones de la siguiente manera:
Finalmente, haz clic en «Aceptar» para generar los resultados de la regresión lineal múltiple.
Paso 6: Interpretar los resultados
Una vez que se hayan calculado los resultados de la regresión, Excel mostrará una tabla con información relevante, como los coeficientes de cada variable independiente, el coeficiente de determinación (R-cuadrado), el error estándar y otros valores estadísticos.
Es importante interpretar adecuadamente estos resultados para comprender la relación entre las variables en estudio. Si tienes dudas sobre cómo interpretar los resultados obtenidos, siempre puedes recurrir a fuentes adicionales como libros de estadística o artículos científicos.
Recuerda que la regresión lineal múltiple en Excel es una herramienta poderosa, pero su correcta interpretación y análisis dependen de un buen conocimiento de estadística y el contexto específico del problema que estás abordando.
¡Ahora estás listo para realizar una regresión lineal múltiple en Excel! Pruébalo con tus propios datos y explora las relaciones entre variables de tu interés.
[automatic_youtube_gallery type=»search» search=»Cómo realizar una regresión lineal múltiple en Excel» limit=»1″]
Cómo realizar una regresión lineal múltiple en Excel
La regresión lineal múltiple es una técnica estadística invaluable que permite estudiar la relación entre una variable dependiente y varias variables independientes. Si te has preguntado cómo desentrañar estas relaciones y obtener predicciones más precisas en tus análisis de datos, este artículo es para ti. Vamos a explorar juntos cómo realizar una regresión lineal múltiple en Excel, una herramienta accesible y ampliamente utilizada en el ámbito empresarial y académico.
¿Qué es la regresión lineal múltiple?
Esta técnica permite analizar la relación existente entre dos o más variables independientes y una variable de respuesta. Por ejemplo, podrías querer entender cómo la cantidad de horas de estudio y la experiencia previa afectan la puntuación de un examen. En el siguiente tutorial, te guiaremos paso a paso para que puedas aplicar esta técnica en Excel.
Pasos para realizar una regresión lineal múltiple en Excel
Paso 1: Preparar los datos
Para iniciar, es fundamental contar con un conjunto de datos organizado. A continuación te indicamos cómo estructurarlo:
- Columna para la variable dependiente (resultado que deseas predecir).
- Columnas separadas para cada variable independiente.
- Los datos deben estar organizados en filas, donde cada fila representa una observación o muestra.
Recuerda que es recomendable tener al menos 30 observaciones para obtener resultados confiables.
Paso 2: Abrir Excel y seleccionar los datos
Una vez que tengas tus datos listos, abre Excel y crea un nuevo libro de trabajo. Selecciona la columna de la variable dependiente y las columnas de las variables independientes manteniendo presionada la tecla Ctrl.
Paso 3: Acceder a la herramienta de Análisis de Datos
Excel ofrece herramientas de análisis que son muy útiles en este proceso. Para acceder a ellas, sigue estos pasos:
- Navega a la pestaña de Datos en la cinta superior de Excel.
- Haz clic en Análisis de Datos. Si no ves esta opción, debes instalar el paquete de herramientas de análisis desde el menú Opciones.
- En la ventana emergente, selecciona Regresión y haz clic en Aceptar.
Paso 4: Configurar la regresión
En la ventana de configuración de la regresión:
- Para Rango de entrada Y, selecciona los datos de la variable dependiente.
- Para Rango de entrada X, selecciona los datos de las variables independientes.
- Marca la casilla de Etiquetas si has incluido los encabezados de las columnas.
- Para Rango de salida, elige una celda donde desees que aparezcan los resultados.
Haz clic en OK y aparecerán los resultados de la regresión.
Paso 5: Interpretar los resultados
Ahora, veamos cómo interpretar los resultados:
- R cuadrado: Indica la proporción de la varianza de la variable dependiente explicada por las independientes.
- Error estándar: Refleja la precisión de tus estimaciones.
- Valores p: Nos dicen si cada variable independiente tiene un efecto significativo en la dependiente.
- Coeficientes: Muestran el impacto esperado en la variable dependiente por cada unidad de cambio en las independientes.
Por ejemplo, si el coeficiente para las horas estudiadas es 5.56, significa que cada hora adicional dedicada a estudiar incrementa la puntuación esperada en 5.56 puntos.
Ejemplo práctico
Imaginemos que estamos analizando cómo las horas de estudio y la cantidad de exámenes de práctica afectan la puntuación en un examen. Siguiendo los pasos anteriores, podemos llegar a una ecuación de regresión que nos permita hacer predicciones basadas en estos factores.
FAQs sobre regresión lineal múltiple en Excel
¿Qué es el coeficiente de determinación (R²)?
El coeficiente de determinación, conocido como R², indica la proporción de la varianza total en la variable dependiente que se puede explicar por las variables independientes en el modelo. Un R² cercano a 1 indica un buen ajuste del modelo, mientras que un valor más bajo sugiere que el modelo no explica adecuadamente la variabilidad de los datos.
¿Por qué es importante comprobar los supuestos de la regresión?
Comprobar los supuestos de la regresión (linealidad, independencia, homocedasticidad y normalidad) es esencial para asegurarte de que los resultados obtenidos sean válidos y confiables. Si alguno de estos supuestos se rompe, podrías obtener estimaciones sesgadas que no reflejan correctamente la relación entre las variables.
¿Puedo realizar regresiones lineales múltiples con variables categóricas?
Sí, puedes incluir variables categóricas en un modelo de regresión lineal múltiple, pero debes convertirlas en variables dummy (0 y 1) para que puedan ser procesadas adecuadamente por el análisis. Esto permite que Excel interprete correctamente estas variables dentro del contexto del modelo.
¿Dónde puedo encontrar más información sobre regresión lineal múltiple?
Para aprender más sobre la regresión lineal múltiple y su aplicación, puedes consultar recursos como la Guía de regresión múltiple de Statistics How To o la sección sobre regresión de Wikipedia.
Conclusión
Realizar una regresión lineal múltiple en Excel es un proceso accesible que puede ofrecerte valiosas perspectivas sobre tus datos. Al seguir los pasos indicados y entender los conceptos detrás de este análisis, estarás mejor preparado para tomar decisiones informadas en base a tus resultados. ¡Empieza a aplicar esta poderosa herramienta en tus análisis hoy mismo!
