¿Alguna vez te has sentido abrumado por un mar de datos en Excel y no sabes por dónde empezar? ¡No estás solo! La regla empírica, también conocida como la regla del 68-95-99.7, puede ser tu mejor aliada para simplificar y entender la distribución de tus datos. En este artículo, te mostraremos cómo aplicar esta poderosa herramienta en Excel, transformando complejas cifras en información clara y procesable. Prepárate para desmitificar tus hojas de cálculo y descubrir patrones ocultos que impulsarán tu análisis al siguiente nivel. ¡Sigue leyendo y conviértete en un maestro de Excel!
Si eres fanático de las matemáticas y te encuentras constantemente trabajando con datos, entonces seguramente conoces la regla empírica. Esta regla tan útil y efectiva nos permite analizar y comprender la distribución de datos en una muestra, ¡y hoy te enseñaremos cómo aplicarla en Excel! Ya sea que estés estudiando estadísticas, trabajando en análisis de datos o simplemente quieras aprender algo nuevo, este artículo te brindará los conocimientos necesarios para utilizar la regla empírica de manera fácil y precisa en esta popular herramienta de hojas de cálculo. ¡No te lo pierdas!
El Regla empíricaa veces denominada regla 68-95-99.7, establece que para un conjunto de datos determinado con una distribución normal:
- 68% de los valores de los datos caen dentro de una desviación estándar de la media.
- 95% de los valores de los datos caen dentro de dos desviaciones estándar de la media.
- 99,7% de los valores de los datos se encuentran dentro de tres desviaciones estándar de la media.
En este tutorial, explicamos cómo aplicar la regla empírica en Excel a un conjunto de datos determinado.
Aplicando la regla empírica en Excel
Supongamos que tenemos un conjunto de datos distribuido normalmente con una media de 7 y una desviación estándar de 2.2. La siguiente captura de pantalla muestra cómo aplicar la regla empírica a este conjunto de datos en Excel para encontrar entre qué valores se encuentra el 68% de los datos, entre qué valores se encuentra el 95% de los datos y entre qué valores se encuentra el 99,7% de los datos:
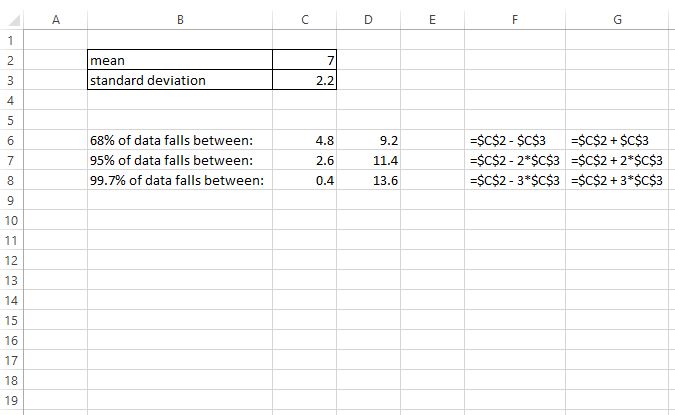
>De esta salida, podemos ver:
- El 68% de los datos se sitúan entre 4.8 y 9.2
- El 95% de los datos se sitúan entre 2.6 y 11.4
- El 99,7% de los datos se sitúan entre 0,4 y 13.6
Las celdas en columnas. F y GRAMO Muestre las fórmulas que se utilizaron para encontrar estos valores.
Para aplicar la regla empírica a un conjunto de datos diferente, simplemente necesitamos cambiar la media y la desviación estándar en las celdas C2 y C3. Por ejemplo, aquí se explica cómo aplicar la regla empírica a un conjunto de datos con una media de 40 y una desviación estándar de 3.75:

>De esta salida, podemos ver:
- El 68% de los datos se sitúan entre 36,25 y 43,75
- El 95% de los datos se sitúan entre 32,5 y 47,5
- El 99,7% de los datos se sitúan entre 28,75 y 51,25
Y aquí hay un ejemplo más de cómo aplicar la regla empírica a un conjunto de datos con una media de 100 y una desviación estándar de 5:
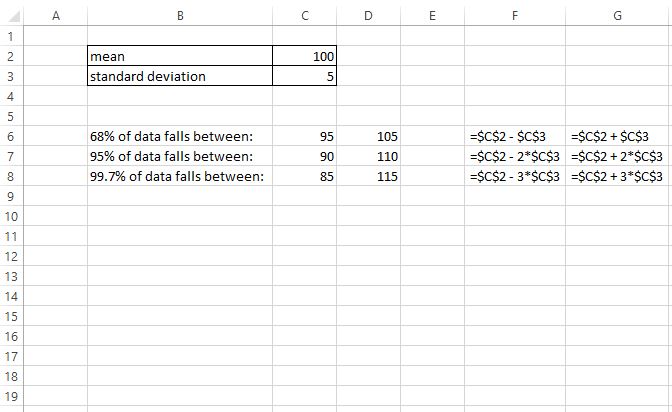
>De esta salida, podemos ver:
- El 68% de los datos se sitúan entre 95 y 105
- El 95% de los datos se sitúan entre 90 y 110
- El 99,7% de los datos se sitúan entre 85 y 115
Encontrar qué porcentaje de datos se encuentra entre ciertos valores
Otra pregunta que podrías tener es: ¿Qué porcentaje de datos se encuentra entre ciertos valores?
Por ejemplo, suponga que tiene un conjunto de datos distribuido normalmente con una media de 100, una desviación estándar de 5 y desea saber qué porcentaje de los datos se encuentra entre los valores. 99 y 105.
En Excel, podemos responder fácilmente a esta pregunta usando la función = DISTR.NORM.()que toma los siguientes argumentos:
DISTR.NORM.(x, media, estándar_dev, acumulativo)
dónde:
- X es el valor que nos interesa
- significar es la media de la distribución
- desarrollo_estándar es la desviación estándar de la distribución
- acumulativo toma un valor de “VERDADERO” (devuelve el CDF) o “FALSO” (devuelve el PDF); usaremos “VERDADERO” para obtener el valor de la función de distribución acumulativa.
La siguiente captura de pantalla muestra cómo utilizar el DISTR.NORMA() función para encontrar el porcentaje de los datos que se encuentran entre los valores 99 y 105 para una distribución que tiene una media de 100 y una desviación estándar de 5:

>Vemos eso 42,1% de los datos se encuentran entre los valores 105 y 99 para esta distribución.
Herramientas útiles:
Calculadora de reglas empíricas
Regla empírica (problemas de práctica)
Cómo aplicar la regla empírica en Excel – Preguntas Frecuentes
Preguntas Frecuentes sobre cómo aplicar la regla empírica en Excel
La regla empírica, también conocida como la regla de 68-95-99.7, es una herramienta estadística que nos permite determinar la probabilidad de un evento en una distribución normal. En Excel, podemos aplicar esta regla utilizando diversas fórmulas y funciones. A continuación, encontrarás respuestas a algunas preguntas frecuentes sobre cómo hacerlo:
1. ¿Qué es la regla empírica?
La regla empírica es una regla estadística utilizada para determinar la probabilidad de un evento en una distribución normal. Se basa en la idea de que aproximadamente el 68% de los datos se encuentra dentro de una desviación estándar de la media, el 95% dentro de dos desviaciones estándar y el 99.7% dentro de tres desviaciones estándar.
2. ¿Cómo calcular la media y la desviación estándar en Excel?
Para calcular la media de un conjunto de datos en Excel, puedes utilizar la función AVERAGE. Por ejemplo, si tus datos se encuentran en la columna A, el siguiente código te dará la media: =AVERAGE(A:A). Para calcular la desviación estándar, puedes utilizar la función STDEV. Siguiendo el mismo ejemplo, el código sería: =STDEV(A:A).
3. ¿Cómo determinar el rango de valores dentro de una desviación estándar?
Para determinar el rango de valores dentro de una desviación estándar en Excel, puedes utilizar fórmulas matemáticas simples. Por ejemplo, si deseas encontrar el rango de valores que se encuentran dentro de una desviación estándar por encima y por debajo de la media, puedes sumar y restar la desviación estándar a la media. El siguiente código muestra cómo hacerlo: =Media±n*Desviación.
4. ¿Cómo encontrar el porcentaje de valores dentro de una desviación estándar?
Para encontrar el porcentaje de valores dentro de una desviación estándar en Excel, puedes utilizar la función NORMDIST. Esta función devuelve la probabilidad acumulada de que un valor esté dentro de un rango específico. Por ejemplo, si deseas calcular el porcentaje de valores dentro de una desviación estándar de la media, puedes usar la siguiente fórmula: =NORMDIST(x,media,desviación,TRUE).
5. ¿Cómo interpretar los resultados?
Los resultados obtenidos al aplicar la regla empírica en Excel te proporcionarán información sobre la distribución de tus datos. Por ejemplo, si el porcentaje de valores dentro de una desviación estándar de la media es cercano al 68%, puedes concluir que tus datos siguen una distribución normal. Si este valor difiere significativamente, podría indicar una distribución atípica.
Esperamos que estas respuestas a las preguntas frecuentes te hayan ayudado a aplicar la regla empírica en Excel. Recuerda que la práctica y la comprensión de los conceptos estadísticos te permitirán usar esta herramienta de forma efectiva.
[automatic_youtube_gallery type=»search» search=»Cómo aplicar la regla empírica en Excel» limit=»1″]
Cómo aplicar la regla empírica en Excel
¿Alguna vez te has sentido abrumado por un mar de datos en Excel y no sabes por dónde empezar? ¡No estás solo! La regla empírica, también conocida como la regla del 68-95-99.7, puede ser tu mejor aliada para simplificar y entender la distribución de tus datos. En este artículo, te mostraremos cómo aplicar esta poderosa herramienta en Excel, transformando complejas cifras en información clara y procesable.
¿Qué es la regla empírica?
La regla empírica es una herramienta estadística fundamental para analizar la distribución de datos en una muestra que sigue una distribución normal. Esta regla establece que:
- 68% de los valores se encuentran dentro de una desviación estándar de la media.
- 95% de los valores se encuentran dentro de dos desviaciones estándar de la media.
- 99.7% de los valores se encuentran dentro de tres desviaciones estándar de la media.
Aplicando la regla empírica en Excel
Supongamos que tienes un conjunto de datos con una media de 7 y una desviación estándar de 2.2. A continuación, te mostramos cómo aplicar la regla empírica en Excel para encontrar entre qué valores se encuentra el 68%, 95% y 99.7% de los datos:
Para calcular estos valores, utiliza las siguientes fórmulas en Excel:
- Para el 68%:
Media - Desviación EstándaryMedia + Desviación Estándar - Para el 95%:
Media - (2 * Desviación Estándar)yMedia + (2 * Desviación Estándar) - Para el 99.7%:
Media - (3 * Desviación Estándar)yMedia + (3 * Desviación Estándar)
Siguiendo este ejemplo, los resultados serían:
- El 68% se sitúa entre 4.8 y 9.2.
- El 95% se sitúa entre 2.6 y 11.4.
- El 99.7% se sitúa entre 0.4 y 13.6.
Ejemplos adicionales de la regla empírica
Para aplicar la regla empírica a otros conjuntos de datos, simplemente cambia la media y la desviación estándar. Aquí algunos ejemplos:
- Media: 40, Desviación Estándar: 3.75.
- Media: 100, Desviación Estándar: 5.
Encontrar el porcentaje de datos entre ciertos valores
Si deseas saber qué porcentaje de datos se encuentra entre dos valores, Excel hace esto sencillo mediante la función DISTR.NORM(). Por ejemplo:
Para un conjunto de datos con media 100 y desviación estándar 5, la fórmula sería:
=DISTR.NORM(105, 100, 5, VERDADERO) - DISTR.NORM(99, 100, 5, VERDADERO)
Esto te dará el porcentaje de datos que caen entre 99 y 105.
Preguntas Frecuentes
¿Qué es la regla empírica?
La regla empírica es una regla que permite determinar la probabilidad de eventos en una distribución normal, informando que aproximadamente el 68% de los datos caen dentro de una desviación estándar de la media, el 95% dentro de dos y el 99.7% dentro de tres.
¿Por qué es útil la regla empírica en Excel?
La regla empírica simplifica la interpretación de conjuntos de datos grandes, permitiendo a los usuarios identificar fácilmente la variabilidad y la probabilidad de eventos en una distribución normal dentro de Excel, una herramienta ampliamente utilizada en análisis de datos.
¿Cómo se pueden visualizar los datos utilizando Excel?
Excel permite visualizar datos de diversas maneras, como mediante gráficos de dispersión, histogramas y gráficos de líneas, lo que facilita la identificación de patrones y tendencias en conjunto con la regla empírica.
Conclusión
Aplicar la regla empírica en Excel te permitirá desmitificar tus hojas de cálculo y analizar datos de manera efectiva. Siguiendo los pasos y ejemplos proporcionados, estarás bien equipado para realizar análisis estadísticos precisos y significativos. ¡No dudes en practicar y explorar las infinitas posibilidades que Excel ofrece!
Para más información, visita Statistics How To.

¡Genial artículo! La regla empírica en Excel me ha salvado en varias ocasiones cuando manejo grandes conjuntos de datos. Una vez, aplicando esta regla, logré simplificar un informe que pensé que me llevaría días, y en solo unas horas estaba listo. ¡Gracias por compartir estos tips! – rubin de celis.
Hormaeche: ¡Totalmente de acuerdo, rubin! La regla empírica es un must en Excel. Yo también la he usado para analizar mis ventas, y te juro que me facilitó un montón las cosas. Un día, al querer presentar un informe a mi jefe, la usé y en un abrir y cerrar de ojos tenía todo muy claro. ¡Esas herramientas hacen la vida más fácil!
Gyhwfanxe: ¡Exacto, rubin! Yo también aprendí a usar la regla empírica y desde entonces no puedo vivir sin ella. Recuerdo que en un proyecto en el que tenía que analizar datos de clientes, me volvió loco tratando de encontrar patrones. Pero una vez la apliqué, todo se volvió pan comido. Me ayudó a tomar decisiones más rápidas y efectivas. ¡Gracias por el artículo, realmente es útil!
Jayellessq: ¡Totalmente de acuerdo con ustedes! La regla empírica me salvó en un momento crucial cuando estaba organizando un evento y tenía que analizar las preferencias de los asistentes. Me costaba un mundo, pero desde que la apliqué, las decisiones se tomaron más rápido y con mucha más claridad. Es una herramienta que vale su peso en oro. ¡Gracias por el artículo, me encanta compartir estas experiencias!