¿Te has preguntado alguna vez cómo puedes desentrañar las relaciones entre variables y hacer predicciones acertadas con tus datos? El análisis de regresión lineal es una poderosa herramienta que te permite hacerlo de manera sencilla, y lo mejor es que puedes llevarlo a cabo con un software que probablemente ya tienes: Excel. En este artículo, exploraremos paso a paso cómo realizar un análisis de regresión lineal en Excel, desglosando sus conceptos clave y proporcionándote ejemplos prácticos que te permitirán tomar decisiones informadas basadas en datos. Prepárate para descubrir el potencial oculto de tus cifras y transformar tu manera de analizar información. ¡Comencemos!
El análisis de regresión lineal es una herramienta fundamental en el campo de la estadística y el modelado de datos. Permite comprender las relaciones entre variables y predecir comportamientos futuros. ¿Sabías que Excel, la popular hoja de cálculo de Microsoft, también puede ser utilizada para realizar este tipo de análisis? En este artículo, exploraremos cómo realizar un análisis de regresión lineal en Excel de manera sencilla y efectiva. Descubre cómo aprovechar al máximo esta potente herramienta y obtén información valiosa a partir de tus datos. ¡No te lo pierdas!
El tutorial explica los conceptos básicos del análisis de regresión y muestra algunas formas diferentes de realizar una regresión lineal en Excel.
Imagínese esto: se le proporciona una gran cantidad de datos diferentes y se le pide que prediga las cifras de ventas del próximo año para su empresa. Ha descubierto docenas, tal vez incluso cientos, de factores que posiblemente pueden afectar los números. Pero ¿cómo saber cuáles son realmente importantes? Ejecute análisis de regresión en Excel. Le dará respuesta a esta y muchas más preguntas: ¿Qué factores importan y cuáles pueden ignorarse? ¿Qué tan estrechamente relacionados están estos factores entre sí? ¿Y qué tan seguro puedes estar de las predicciones?
Análisis de regresión en Excel: conceptos básicos
En el modelado estadístico, análisis de regresión se utiliza para estimar las relaciones entre dos o más variables:
Variable dependiente (también conocido como criterio variable) es el factor principal que está tratando de comprender y predecir.
Variables independientes (también conocido como explicativo variables, o predictores) son los factores que podrían influir en la variable dependiente.
El análisis de regresión ayuda a comprender cómo cambia la variable dependiente cuando varía una de las variables independientes y permite determinar matemáticamente cuál de esas variables realmente tiene un impacto.
Técnicamente, un modelo de análisis de regresión se basa en la suma de cuadrados, que es una forma matemática de encontrar la dispersión de puntos de datos. El objetivo de un modelo es obtener la suma de cuadrados más pequeña posible y trazar la línea que más se acerque a los datos.
En estadística, diferencian entre regresión lineal simple y múltiple. Regresión lineal simple modela la relación entre una variable dependiente y una variable independiente utilizando una función lineal. Si utiliza dos o más variables explicativas para predecir la variable dependiente, se trata de regresión lineal múltiple. Si la variable dependiente se modela como una función no lineal porque las relaciones de datos no siguen una línea recta, use regresión no lineal en cambio. El objetivo de este tutorial será una regresión lineal simple.
Como ejemplo, tomemos las cifras de ventas de paraguas de los últimos 24 meses y averigüemos la precipitación mensual promedio durante el mismo período. Trace esta información en un gráfico y la línea de regresión demostrará la relación entre la variable independiente (lluvias) y la variable dependiente (ventas generales):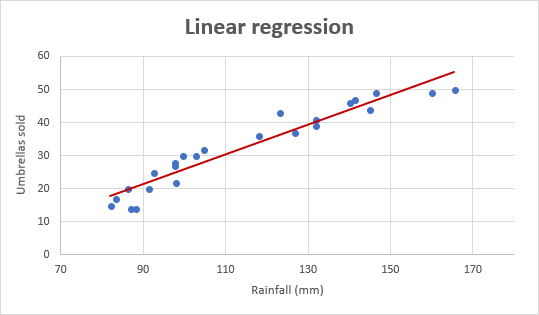
>Ecuación de regresión lineal
Matemáticamente, una regresión lineal se define mediante esta ecuación:
y = bx + a + ε
Dónde:
- X es una variable independiente.
- y es una variable dependiente.
- a es el Intersección en Yque es el valor medio esperado de y cuando todo X las variables son iguales a 0. En un gráfico de regresión, es el punto donde la línea cruza el eje Y.
- b es el pendiente de una línea de regresión, que es la tasa de cambio para y como X cambios.
- ε es el término de error aleatorio, que es la diferencia entre el valor real de una variable dependiente y su valor previsto.
La ecuación de regresión lineal siempre tiene un término de error porque, en la vida real, los predictores nunca son perfectamente precisos. Sin embargo, algunos programas, incluido Excel, calculan el término de error entre bastidores. Entonces, en Excel, se hace una regresión lineal usando el mínimos cuadrados método y buscar coeficientes a y b tal que:
y = bx + a
Para nuestro ejemplo, la ecuación de regresión lineal toma la siguiente forma:
Umbrellas sold = b * rainfall + a
Existen varias formas diferentes de encontrar a y b. Los tres métodos principales para realizar análisis de regresión lineal en Excel son:
- Herramienta de regresión incluida con Analysis ToolPak
- Gráfico de dispersión con una línea de tendencia
- Fórmula de regresión lineal
A continuación encontrará instrucciones detalladas sobre el uso de cada método.
Este ejemplo muestra cómo ejecutar la regresión en Excel utilizando una herramienta especial incluida con el complemento Herramientas de análisis.
Habilite el complemento Analysis ToolPak
Herramientas de análisis está disponible en todas las versiones de Excel 365 a 2003, pero no está habilitado de forma predeterminada. Por lo tanto, debes activarlo manualmente. Así es cómo:
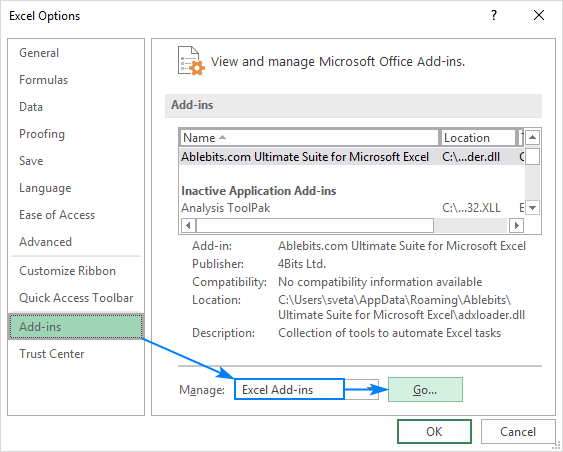
>
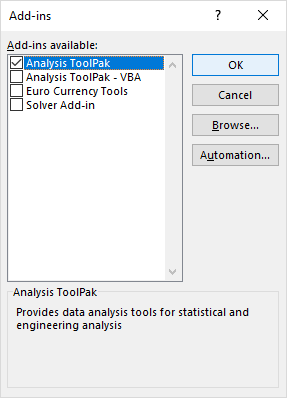
>
Esto agregará el Análisis de los datos herramientas para el Datos pestaña de su cinta de Excel.
Ejecutar análisis de regresión
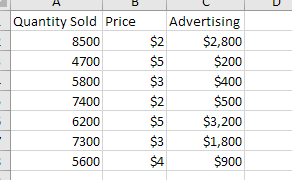
En este ejemplo, vamos a hacer una regresión lineal simple en Excel. Lo que tenemos es una lista de precipitaciones mensuales promedio durante los últimos 24 meses en la columna B, que es nuestra variable independiente (predictora), y el número de paraguas vendidos en la columna C, que es la variable dependiente. Por supuesto, hay muchos otros factores que pueden afectar las ventas, pero por ahora nos centraremos sólo en estas dos variables: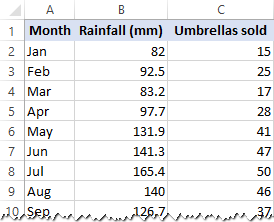
>
Con Analysis Toolpak agregado habilitado, lleve a cabo estos pasos para realizar un análisis de regresión en Excel:
>
>
- Selecciona el Rango de entrada Ycual es tuyo variable dependiente. En nuestro caso, se trata de ventas paraguas (C1:C25).
- Selecciona el Rango de entrada Xes decir, tu variable independiente. En este ejemplo, es la precipitación mensual promedio (B1:B25).
Si está creando un modelo de regresión múltiple, seleccione dos o más columnas adyacentes con diferentes variables independientes.
- Comprobar el Caja de etiquetas si hay encabezados en la parte superior de los rangos X e Y.
- Elige tu preferido opción de salida, una nueva hoja de trabajo en nuestro caso.
- Opcionalmente, seleccione el Derechos residuales de autor casilla de verificación para obtener la diferencia entre los valores previstos y reales.

>
Interpretar el resultado del análisis de regresión
Como acaba de ver, ejecutar la regresión en Excel es fácil porque todos los cálculos se realizan automáticamente. La interpretación de los resultados es un poco más complicada porque es necesario saber qué hay detrás de cada número. A continuación encontrará un desglose de 4 partes principales del resultado del análisis de regresión.
Resultado del análisis de regresión: resultado resumido
Esta parte le indica qué tan bien se ajusta la ecuación de regresión lineal calculada a sus datos de origen.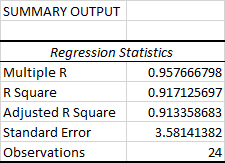
>
Esto es lo que significa cada dato:
Múltiples R. es la ccoeficiente de relación que mide la fuerza de una relación lineal entre dos variables. El coeficiente de correlación puede tener cualquier valor entre -1 y 1, y su valor absoluto indica la fuerza de la relación. Cuanto mayor sea el valor absoluto, más fuerte será la relación:
- 1 significa una fuerte relación positiva
- -1 significa una fuerte relación negativa
- 0 significa que no hay ninguna relación
R Plaza. Es el Coeficiente de determinación, que se utiliza como indicador de la bondad del ajuste. Muestra cuántos puntos caen en la recta de regresión. El r2 El valor se calcula a partir de la suma total de cuadrados, más precisamente, es la suma de las desviaciones al cuadrado de los datos originales de la media.
En nuestro ejemplo, R2 es 0,91 (redondeado a 2 dígitos), lo cual es bastante bueno. Significa que el 91% de nuestros valores se ajustan al modelo de análisis de regresión. En otras palabras, el 91% de las variables dependientes (valores de y) se explican por las variables independientes (valores de x). Generalmente, un R cuadrado de 95% o más se considera un buen ajuste.
Cuadrado R ajustado. Es el R Plaza ajustado por el número de variables independientes en el modelo. Querrá utilizar este valor en lugar de R Plaza para análisis de regresión múltiple.
Error estándar. Es otra medida de bondad de ajuste que muestra la precisión de su análisis de regresión: cuanto menor sea el número, más seguro podrá estar acerca de su ecuación de regresión. mientras que r2 representa el porcentaje de la varianza de las variables dependientes que explica el modelo, el error estándar es una medida absoluta que muestra la distancia promedio a la que caen los puntos de datos desde la línea de regresión.
Observaciones. Es simplemente el número de observaciones en su modelo.
Resultado del análisis de regresión: ANOVA
La segunda parte del resultado es el Análisis de Varianza (ANOVA):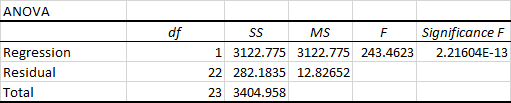
>
Básicamente, divide la suma de cuadrados en componentes individuales que brindan información sobre los niveles de variabilidad dentro de su modelo de regresión:
- df es el número de grados de libertad asociados con las fuentes de varianza.
- SS es la suma de cuadrados. Cuanto más pequeño sea el SS residual en comparación con el SS total, mejor se ajustará su modelo a los datos.
- EM es el cuadrado medio.
- F es el estadístico F, o prueba F para la hipótesis nula. Se utiliza para probar la importancia general del modelo.
- Significado F es el valor P de F.
La parte ANOVA rara vez se usa para un análisis de regresión lineal simple en Excel, pero definitivamente deberías observar de cerca el último componente. El Significado F El valor da una idea de cuán confiables (estadísticamente significativos) son sus resultados. Si la significancia F es inferior a 0,05 (5%), su modelo está bien. Si es mayor que 0,05, probablemente será mejor que elijas otra variable independiente.
Resultado del análisis de regresión: coeficientes
Esta sección proporciona información específica sobre los componentes de su análisis:
>
El componente más útil en esta sección es Coeficientes. Le permite construir un ecuación de regresión lineal en Excel:
y = bx + a
Para nuestro conjunto de datos, donde y es el número de paraguas vendidos y x es la precipitación mensual promedio, nuestra fórmula de regresión lineal es la siguiente:
Y = Rainfall Coefficient * x + Intercept
Equipado con valores de a y b redondeados a tres decimales, se convierte en:
Y=0.45*x-19.074
Por ejemplo, con una precipitación media mensual de 82 mm, las ventas totales serían aproximadamente 17,8:
0.45*82-19.074=17.8
De manera similar, puedes saber cuántos paraguas se van a vender con cualquier otra precipitación mensual (x variable) que especifiques.
Salida del análisis de regresión: residuos
Si compara el número estimado y real de paraguas vendidos correspondientes a una precipitación mensual de 82 mm, verá que estos números son ligeramente diferentes:
- Estimado: 17,8 (calculado arriba)
- Real: 15 (fila 2 de los datos de origen)
¿Por qué es la diferencia? Porque las variables independientes nunca son predictores perfectos de las variables dependientes. Y los residuales pueden ayudarle a comprender qué tan lejos están los valores reales de los valores predichos: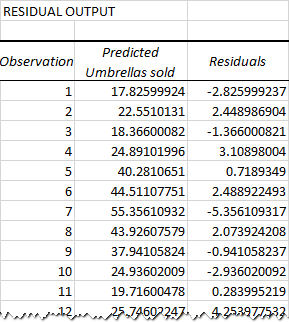
>
Para el primer punto de datos (precipitaciones de 82 mm), el residuo es aproximadamente -2,8. Entonces, sumamos este número al valor previsto y obtenemos el valor real: 17,8 – 2,8 = 15.
Cómo hacer un gráfico de regresión lineal en Excel
Si necesita visualizar rápidamente la relación entre las dos variables, dibuje un gráfico de regresión lineal. ¡Eso es muy fácil! Así es cómo:

> Esto insertará un diagrama de dispersión en su hoja de trabajo, que se parecerá a este:
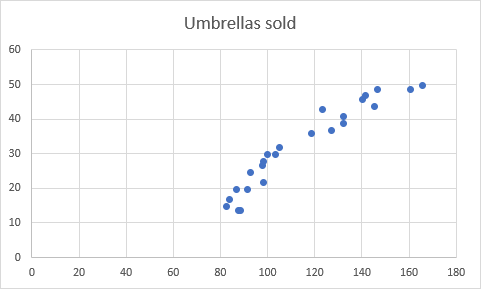
>
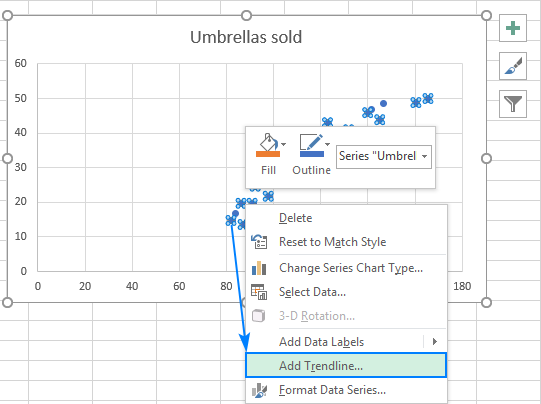
>
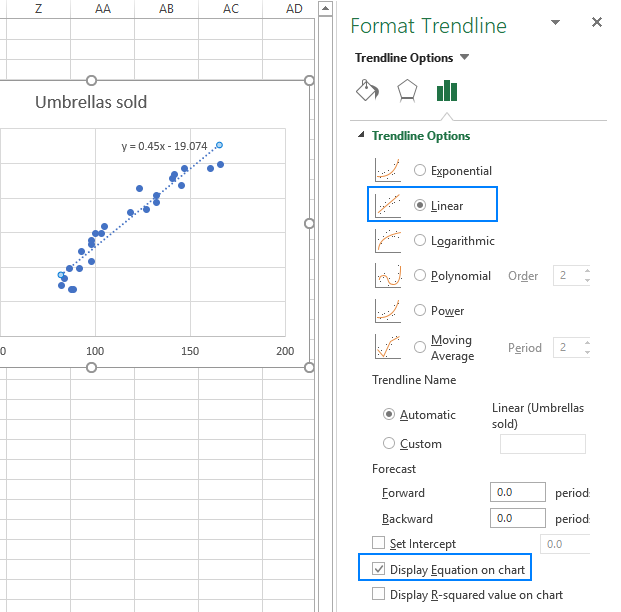
> Como puede notar, la ecuación de regresión que Excel ha creado para nosotros es la misma que la fórmula de regresión lineal que construimos en base a la Salida de coeficientes.
>
En este punto, su gráfico ya parece un gráfico de regresión decente: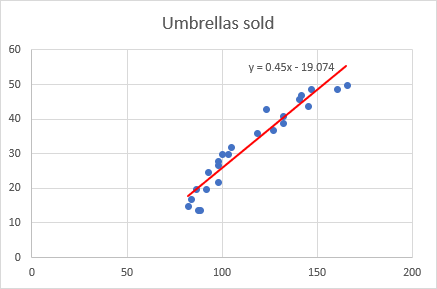
>
Aun así, es posible que desees realizar algunas mejoras más:
Cómo hacer regresión en Excel usando fórmulas
Microsoft Excel tiene algunas funciones estadísticas que pueden ayudarle a realizar análisis de regresión lineal, como ESTIMACIÓN LINEAL, PENDIENTE, INTERCEPCIÓN y CORREL.
La función ESTIMACIÓN LINEAL utiliza el método de regresión de mínimos cuadrados para calcular una línea recta que explica mejor la relación entre las variables y devuelve una matriz que describe esa línea. Puede encontrar la explicación detallada de la sintaxis de la función en este tutorial. Por ahora, simplemente hagamos una fórmula para nuestro conjunto de datos de muestra:
=LINEST(C2:C25, B2:B25)
Debido a que la función ESTIMACIÓN LINEAL devuelve una matriz de valores, debe ingresarla como una fórmula matricial. Seleccione dos celdas adyacentes en la misma fila, E2: F2 en nuestro caso, escriba la fórmula y presione Ctrl + Mayús + Intro para completarlo.
La fórmula devuelve el b coeficiente (E1) y el a constante (F1) para la ya familiar ecuación de regresión lineal:
y = bx + a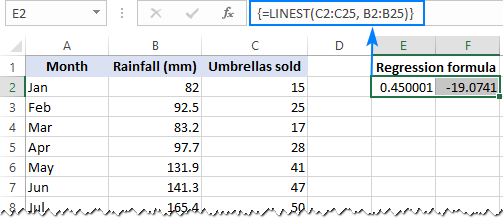
>
Si evita el uso de fórmulas matriciales en sus hojas de trabajo, puede calcular a y b individualmente con fórmulas regulares:
Obtenga la intersección en Y (a):
=INTERCEPT(C2:C25, B2:B25)
Obtenga la pendiente (b):
=SLOPE(C2:C25, B2:B25)
Además, puede encontrar el coeficiente de correlación (Múltiples R en el análisis de regresión salida resumida) que indica qué tan fuertemente están relacionadas las dos variables entre sí:
=CORREL(B2:B25,C2:C25)
La siguiente captura de pantalla muestra todas estas fórmulas de regresión de Excel en acción: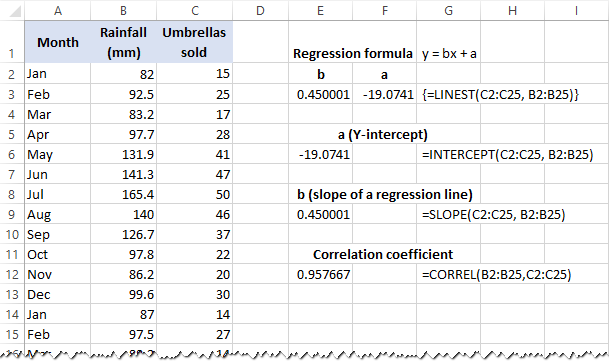
>
Consejo. Si desea obtener estadísticas adicionales para su análisis de regresión, utilice la función ESTIMACIÓN LINEAL con el statuajes parámetro establecido en TRUE como se muestra en este ejemplo.
Así es como se hace la regresión lineal en Excel. Dicho esto, tenga en cuenta que Microsoft Excel no es un programa estadístico. Si necesita realizar un análisis de regresión a nivel profesional, es posible que desee utilizar software específico como XLSTAT, Regresiónetc.
Para ver más de cerca nuestras fórmulas de regresión lineal y otras técnicas analizadas en este tutorial, puede descargar nuestro libro de trabajo de muestra a continuación. ¡Gracias por leer!
Libro de práctica
Análisis de regresión en Excel: ejemplos (archivo .xlsx)
Usted también podría estar interesado en
Análisis de regresión lineal en Excel – Preguntas frecuentes
Preguntas frecuentes sobre el análisis de regresión lineal en Excel
¿Qué es el análisis de regresión lineal en Excel?
El análisis de regresión lineal en Excel es una técnica estadística que permite examinar la relación entre una variable independiente y una variable dependiente. Se utiliza para predecir el valor de una variable en función de otra utilizando una línea recta que representa la relación entre ambas variables.
¿Cuáles son los pasos para realizar un análisis de regresión lineal en Excel?
¿Cuál es el coeficiente de determinación en un análisis de regresión lineal?
El coeficiente de determinación, representado como R², es una medida de la bondad de ajuste de la regresión lineal. Indica qué porcentaje de la variabilidad de la variable dependiente puede explicarse por la variable independiente en el modelo de regresión lineal. Un valor de R² cercano a 1 indica un buen ajuste del modelo, mientras que un valor cercano a 0 indica que el modelo no explica bien los datos.
¿Existen otros tipos de análisis de regresión en Excel?
Sí, aparte de la regresión lineal, Excel ofrece otros tipos de análisis de regresión, como la regresión logística, la regresión polinómica y la regresión exponencial. Estos tipos de análisis de regresión pueden utilizarse según la naturaleza de los datos y el objetivo del estudio.
¿Dónde puedo encontrar más información sobre el análisis de regresión lineal en Excel?
Puedes encontrar más información detallada sobre el análisis de regresión lineal en Excel en los siguientes recursos:
[automatic_youtube_gallery type=»search» search=»Análisis de regresión lineal en Excel.» limit=»1″]
La regresión lineal en Excel es una técnica poderosa que permite analizar la relación entre una variable independiente (predictora) y una variable dependiente (respuesta). A continuación, se presenta un resumen de los pasos para realizar un análisis de regresión lineal en Excel, así como su interpretación.
Pasos para realizar un análisis de regresión lineal en Excel
- Habilitar el complemento de Herramientas de Análisis:
- Ve a «Archivo» > «Opciones» > «Complementos».
– En el cuadro «Administrar», selecciona «Complementos de Excel» y haz clic en «Ir».
– En el cuadro de diálogo de Complementos, marca «Herramientas para Análisis» y haz clic en «Aceptar».
- Preparar los datos:
– Organiza tus datos en columnas, asegurándote de que la variable independiente (X) y la variable dependiente (Y) estén correctamente etiquetadas. Por ejemplo:
– Columna B: Precipitaciones mensuales promedio (X).
– Columna C: Ventas de paraguas (Y).
- Ejecutar el análisis de regresión:
– Haz clic en la pestaña «Datos» en la cinta de opciones.
– En el grupo «Análisis», selecciona «Análisis de Datos».
– Escoge «Regresión» y haz clic en «Aceptar».
- Configura los rangos:
– Rango de entrada Y: Selecciona tu variable dependiente (C1:C25).
– Rango de entrada X: Selecciona tu variable independiente (B1:B25).
– Marca la casilla «Etiquetas» si incluyes encabezados en tus datos.
– Elige una ubicación para el resultado (nueva hoja de trabajo).
– Opcionalmente, marca »Residuos» para obtener el análisis de residuos.
– Haz clic en «Aceptar».
Interpretación de los resultados
Los resultados del análisis de regresión se dividen en varias secciones clave que debes interpretar:
- Resumen del resultado:
– Múltiples R: Correlación entre las variables; valores cercanos a 1 o -1 indican una fuerte relación.
– R cuadrado (R²): Proporción de varianza en la Y explicada por la X; valores cercanos a 1 indican un buen ajuste del modelo.
- Error estándar: Indica la precisión del modelo; un valor más bajo sugiere un mejor ajuste.
- Observaciones: Cantidad de datos analizados.
- ANOVA:
– Evalúa la variabilidad y significancia del modelo.
– Significancia F: Un valor inferior a 0,05 generalmente indica que el modelo es estadísticamente significativo.
- Coeficientes:
– Proporciona los valores de a (intercepción) y b (pendiente) para formar la ecuación de la recta: y = bx + a.
– Por ejemplo, si obtienes un coeficiente de pendiente de 0.45 y una intercepción de -19.074, la fórmula resultante sería:
– Y = 0.45*X - 19.074.
- Residuos:
– La diferencia entre los valores observados y predichos. Un análisis de residuos puede ayudar a identificar outliers o patrones no capturados por el modelo.
Visualización de la regresión lineal
Para representar gráficamente la relación entre las variables:
- Selecciona los datos de X e Y.
- Ve a la pestaña «Insertar», selecciona «Gráficos» y elige un gráfico de dispersión.
- Haz clic derecho en algún punto del gráfico, selecciona «Agregar línea de tendencia» y elige «Lineal».
- Puedes habilitar la opción «Mostrar ecuación en el gráfico» para ver la fórmula de regresión.
Cálculos de regresión usando fórmulas
Además del análisis de herramientas, también puedes usar funciones de Excel como:
=LINEST(Yrango, Xrango)para obtener la pendiente y la intercepción.=SLOPE(Yrango, Xrango)para la pendiente.=INTERCEPT(Yrango, Xrango)para la intercepción.=CORREL(Xrango, Yrango)para obtener la correlación.
Conclusión
El análisis de regresión lineal en Excel es accesible y permite insights valiosos sobre la relación entre variables. Sin embargo, es importante complementarlo con un entendimiento de los fundamentos estadísticos para interpretar correctamente los resultados. Si se necesita un análisis más avanzado, considerar software estadístico especializado puede ser recomendable.

TholoiI: ¡Hola a todos! Me encanta ver que estamos en la misma sintonía. A mí me pasó algo similar, en la uni me tocó usar regresión lineal para un proyecto de estadística, y aunque al principio fue un dolor de cabeza, gracias a Excel al final me ayudó a entender mejor mis datos. ¡Definitivamente es una herramienta que hace la vida más fácil!
Mandado: ¡Hola, DorantiniV y lezshtatZ! Estoy con ustedes, el artículo está increíble. Yo también me acuerdo cuando tuve que hacer un trabajito de fin de curso y descubrí la regresión lineal en Excel. La verdad, al principio me daba un poco de pereza, pero luego fue muy útil para mis análisis. ¡Excel hizo el trabajo mucho más liviano y hasta divertido! ¡Saludos!
LezshtatZ: ¡Totalmente de acuerdo, DorantiniV! El análisis de regresión puede ser complicado al principio, pero una vez que le agarras la onda, es súper útil. Yo lo usé para analizar datos de ventas en mi trabajo y me ayudó a tomar decisiones más acertadas. Excel lo simplifica tanto, ¡así que a darle!
DorantiniV: ¡Genial el artículo! Me encantó cómo explicaste el análisis de regresión lineal, me trae recuerdos de cuando lo usé para mi proyecto de clase, aunque al principio me costó un montón entenderlo. Excel lo hace mucho más fácil. ¡Gracias por compartir!