¿Te has preguntado alguna vez cómo los estadísticos logran convertir grandes volúmenes de datos en conclusiones comprensibles? Una de las herramientas más poderosas en este proceso es el Teorema del Límite Central. En este artículo, te mostraremos de manera sencilla y práctica cómo aplicar este teorema utilizando Excel, permitiéndote desentrañar patrones ocultos en tus datos y tomar decisiones más informadas. Ya seas un estudiante, un profesional o simplemente un entusiasta de la estadística, descubrirás que dominar este concepto puede transformar tu enfoque analítico. ¡Prepárate para llevar tus habilidades con Excel al siguiente nivel!
El teorema del límite central (TLC) es un concepto fundamental en la estadística que permite hacer inferencias sobre una población a partir de muestras aleatorias. Aunque suena complicado, ¡no te preocupes! En este artículo te mostraremos cómo aplicar el TLC de manera sencilla y práctica utilizando una herramienta que todos conocemos: ¡Excel! Descubre cómo esta poderosa herramienta puede facilitarte la aplicación del teorema del límite central y hacer de tus análisis estadísticos un proceso mucho más eficiente. Sigue leyendo para aprender todos los detalles sobre este tema tan interesante.
El teorema del límite central establece que la distribución muestral de una media muestral es aproximadamente normal si el tamaño de la muestra es lo suficientemente grande, incluso si la distribución de la población no es normal.
El teorema del límite central también establece que la distribución muestral tendrá las siguientes propiedades:
1. La media de la distribución muestral será igual a la media de la distribución poblacional:
x = µ
2. La desviación estándar de la distribución muestral será igual a la desviación estándar de la población dividida por el tamaño de la muestra:
s = s / √norte
En este tutorial, explicamos cómo aplicar el teorema del límite central en Excel a una distribución determinada.
Aplicar el teorema del límite central en Excel
Supongamos que tenemos una distribución con una media de 8 y una desviación estándar de 4. Podemos usar las siguientes fórmulas en Excel para encontrar tanto la media como la desviación estándar de la distribución muestral con un tamaño de muestra de 15:
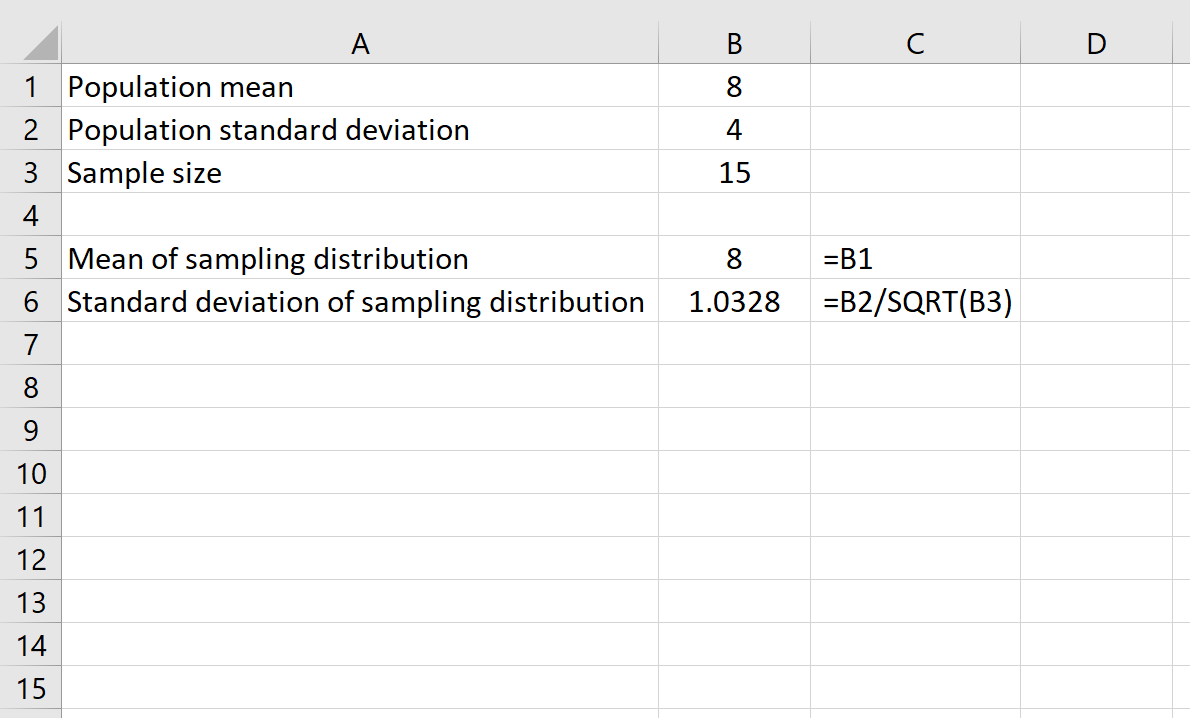
>La media de la distribución muestral es simplemente igual a la media de la distribución poblacional, que es 8.
La desviación estándar de la distribución muestral es igual a la desviación estándar de la población dividida por el tamaño de la muestra, que es: 4 /√15 = 1.0328.
También podemos usar el teorema del límite central para responder preguntas sobre probabilidades. Por ejemplo, si una población dada tiene una media de 8 y una desviación estándar de 4¿cuál es la probabilidad de que una muestra dada de tamaño 15 tiene una media menor o igual a 7?
Para responder a esta pregunta podemos utilizar el DISTR.NORMA() función en Excel, que utiliza la siguiente sintaxis:
DISTR.NORM(x, media, desv_estándar, acumulativo)
dónde:
- X: la muestra significa que le gustaría probar
- significar: media esperada de la distribución muestral
- desarrollo_estándar: desviación estándar esperada de la distribución muestral
- acumulativo: VERDADERO devuelve el valor del CDF normal; FALSO devuelve el valor del PDF normal. En nuestro caso siempre usaremos VERDADERO.
Esta función devolverá la probabilidad de que la media muestral sea menor o igual a un determinado valor.
Aquí está la fórmula que usaríamos en este ejemplo:
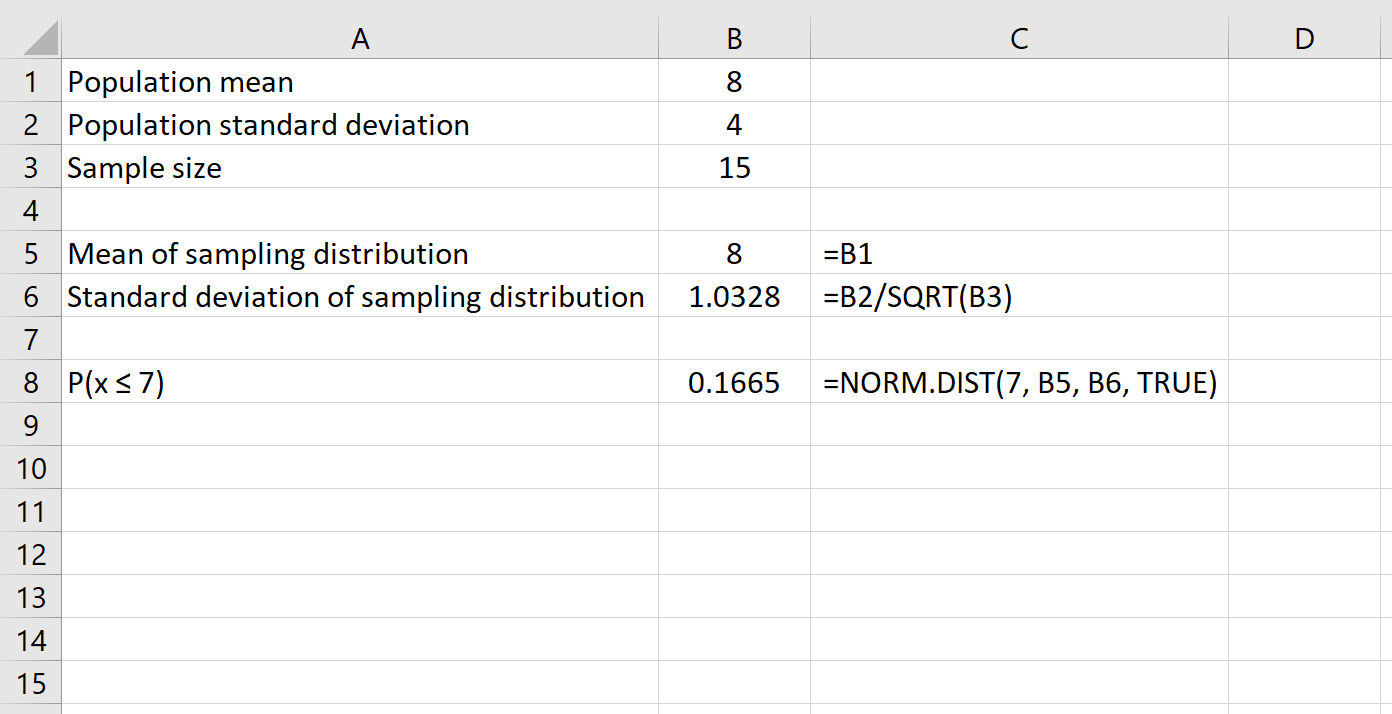
>Esto nos dice que para una población con una media de 8 y una desviación estándar de 4la probabilidad de que una muestra dada de tamaño 15 tiene una media menor o igual a 7 es 0.1665.
También podemos encontrar la probabilidad de que un tamaño de muestra dado tenga una media mayor que que un cierto número simplemente usando la fórmula 1 – DISTR.NORM.().
Por ejemplo, la siguiente fórmula muestra cómo encontrar la probabilidad de que un tamaño de muestra dado de 15 tenga una media mas grande que 7:
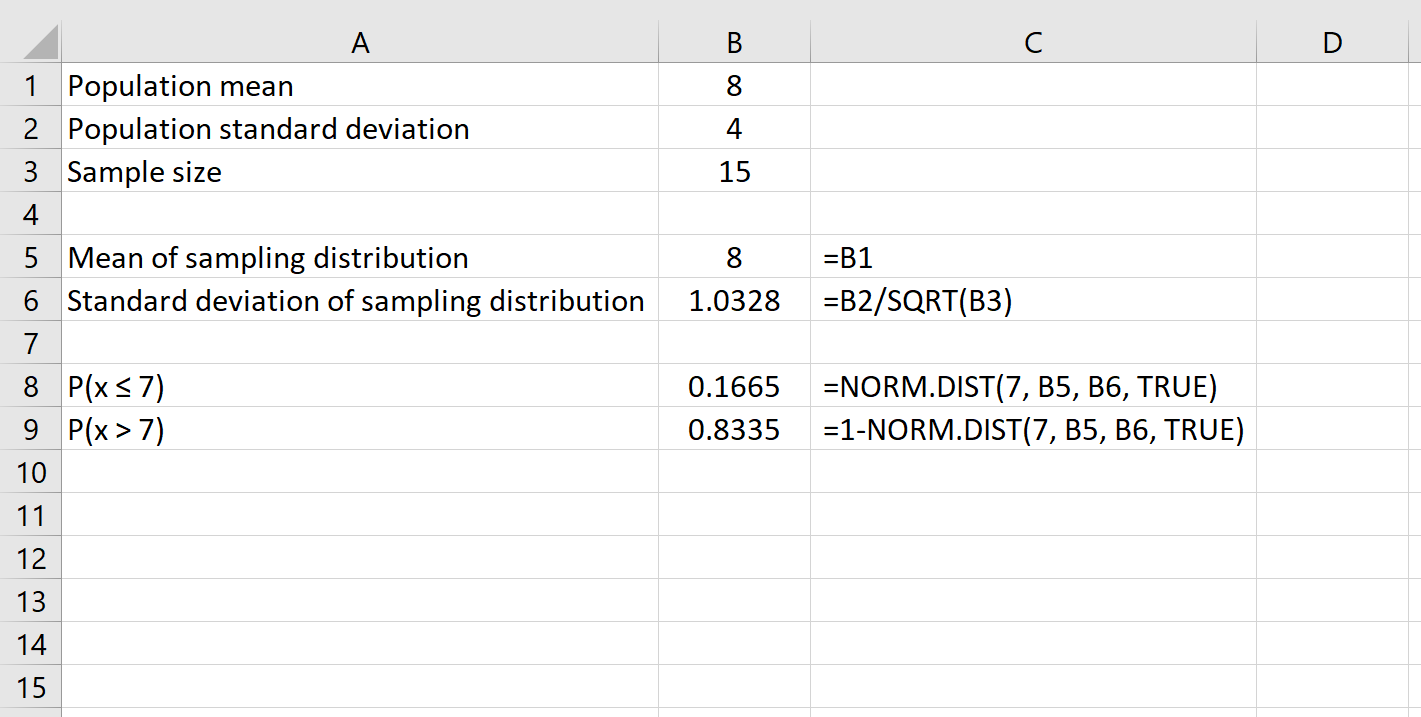
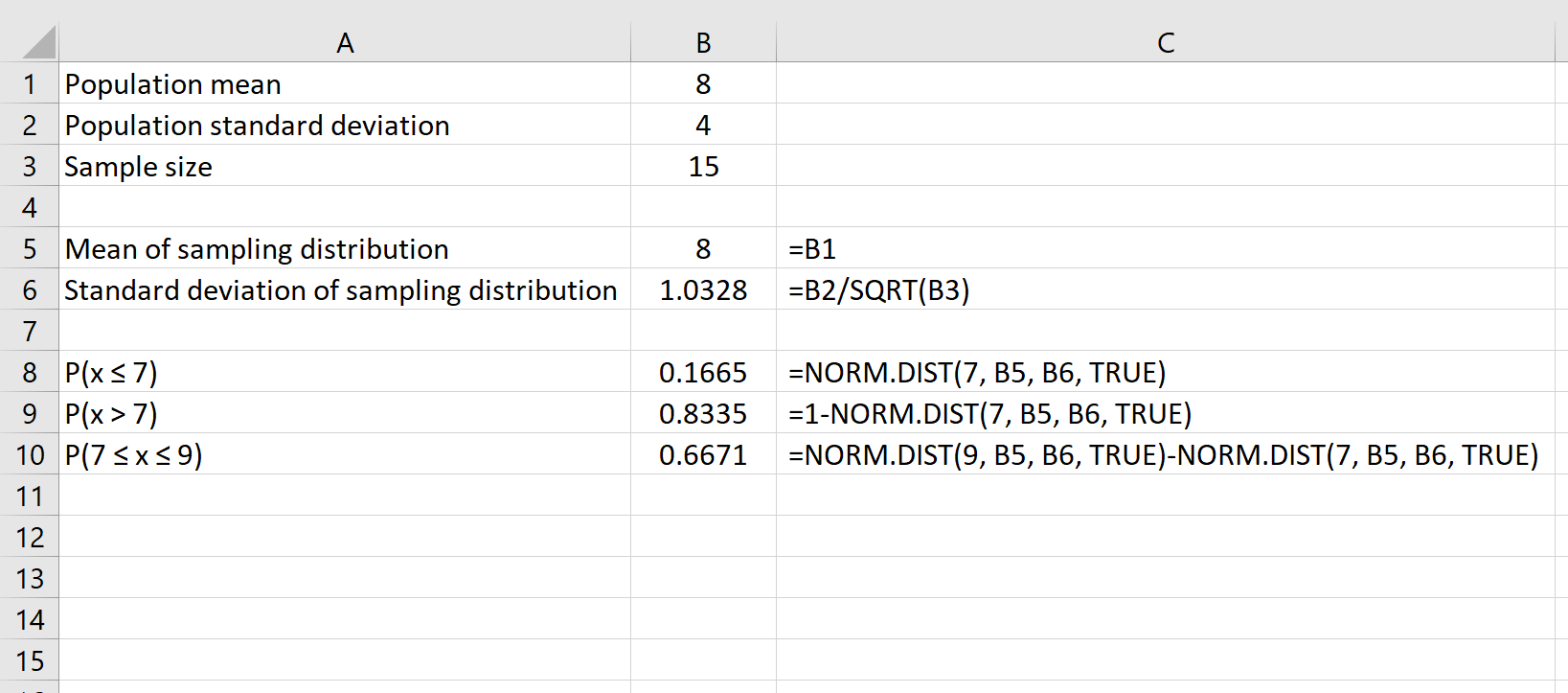
>Por último, podemos encontrar la probabilidad de que un tamaño de muestra dado tenga una media entre dos números usando la fórmula DISTR.NORM.(número mayor) – DISTR.NORM.(número menor).
Por ejemplo, la siguiente fórmula muestra cómo encontrar la probabilidad de que un tamaño de muestra dado de 15 tenga una media entre 7 y 9:
>Recursos adicionales
Calculadora del teorema del límite central
Cómo aplicar la regla empírica en Excel
Cómo hacer una curva de campana en Excel
Cómo aplicar el teorema del límite central en Excel – Preguntas frecuentes
Preguntas frecuentes sobre cómo aplicar el teorema del límite central en Excel
1. ¿Qué es el teorema del límite central?
El teorema del límite central es un concepto fundamental en estadística que establece que, bajo ciertas condiciones, la distribución de la media muestral de cualquier población tiende a aproximarse a una distribución normal. Este teorema es ampliamente utilizado para realizar inferencias estadísticas y estimaciones de parámetros poblacionales.
2. ¿Cuál es la importancia de aplicar el teorema del límite central en Excel?
Aplicar el teorema del límite central en Excel permite obtener resultados precisos y confiables al analizar muestras de datos. Excel es una herramienta versátil que brinda funciones estadísticas y gráficas, lo que facilita el cálculo y la representación visual de los resultados.
3. ¿Cuáles son los pasos para aplicar el teorema del límite central en Excel?
4. ¿Existen herramientas adicionales en Excel para aplicar el teorema del límite central?
Sí, Excel ofrece diversas herramientas que facilitan la aplicación del teorema del límite central, como las funciones de distribución normal (NORM.DIST) y la generación de números aleatorios (ALEATORIO.ENTRE).
5. ¿Dónde puedo encontrar más información sobre el teorema del límite central y su aplicación en Excel?
Si deseas obtener más información sobre el teorema del límite central y su aplicación en Excel, te recomendamos consultar las siguientes fuentes:
- Wikipedia – Teorema del límite central
- Soporte de Microsoft – Función TEORESULTADO
- Excel Total – Teorema del límite central en Excel
[automatic_youtube_gallery type=»search» search=»Cómo aplicar el teorema del límite central en Excel» limit=»1″]
Cómo aplicar el teorema del límite central en Excel
¿Te has preguntado alguna vez cómo los estadísticos logran transformar grandes volúmenes de datos en conclusiones comprensibles? Una de las herramientas más poderosas en este proceso es el Teorema del Límite Central (TLC). En este artículo, te mostraremos de manera sencilla y práctica cómo aplicar este teorema utilizando Excel, permitiéndote desentrañar patrones ocultos en tus datos y tomar decisiones más informadas.
¿Qué es el Teorema del Límite Central?
El teorema del límite central es un concepto fundamental en la estadística que establece que la distribución muestral de una media muestral es aproximadamente normal si el tamaño de la muestra es suficientemente grande, incluso si la distribución de la población no es normal.
Propiedades del Teorema del Límite Central
- La media de la distribución muestral será igual a la media de la distribución poblacional: x = µ.
- La desviación estándar de la distribución muestral será igual a la desviación estándar de la población dividida por el tamaño de la muestra: s = s / √n.
Aplicar el Teorema del Límite Central en Excel
Supongamos que tenemos una distribución con una media de 8 y una desviación estándar de 4. Podemos usar las siguientes fórmulas en Excel para encontrar tanto la media como la desviación estándar de la distribución muestral con un tamaño de muestra de 15:
- La media de la distribución muestral es simplemente igual a la media de la distribución poblacional, que es 8.
- La desviación estándar de la distribución muestral es igual a la desviación estándar de la población dividida por el tamaño de la muestra, que es: 4 / √15 ≈ 1.0328.
Cálculo de probabilidades con el TLC en Excel
También podemos usar el teorema del límite central para responder preguntas sobre probabilidades. Por ejemplo, si una población dada tiene una media de 8 y una desviación estándar de 4, ¿cuál es la probabilidad de que una muestra de tamaño 15 tenga una media menor o igual a 7?
Para responder a esta pregunta, puedes utilizar la función DISTR.NORM() en Excel, que utiliza la siguiente sintaxis:
DISTR.NORM(x, media, desv_estándar, acumulativo)
Donde:
- x: El valor que deseas probar.
- media: Media esperada de la distribución muestral.
- desv_estándar: Desviación estándar esperada de la distribución muestral.
- acumulativo: VERDADERO devuelve el valor del CDF normal; FALSO devuelve el valor del PDF normal.
En nuestro caso, siempre usaremos VERDADERO. Aquí está la fórmula que usaríamos en este ejemplo para calcular la probabilidad:
DISTR.NORM(7, 8, 1.0328, VERDADERO) que nos dice que para una población con una media de 8 y una desviación estándar de 4, la probabilidad de que una muestra de tamaño 15 tenga una media menor o igual a 7 es aproximadamente 0.1665.
Más aplicaciones en Excel
Podemos encontrar la probabilidad de que una muestra de tamaño dado tenga una media mayor que un cierto número utilizando la fórmula:
1 – DISTR.NORM()
Por ejemplo, para encontrar la probabilidad de que una muestra de tamaño 15 tenga una media mayor que 7:
1 – DISTR.NORM(7, 8, 1.0328, VERDADERO) que devuelve la probabilidad complementaria.
Además, podemos determinar la probabilidad de que una muestra tenga una media entre dos números empleando la fórmula:
DISTR.NORM(número mayor) - DISTR.NORM(número menor).
Por ejemplo, para encontrar la probabilidad de que una muestra de tamaño 15 tenga una media entre 7 y 9:
DISTR.NORM(9, 8, 1.0328, VERDADERO) – DISTR.NORM(7, 8, 1.0328, VERDADERO).
Recursos adicionales
- Calculadora del Teorema del Límite Central
- Cómo aplicar la regla empírica en Excel
- Cómo hacer una curva de campana en Excel
Preguntas frecuentes
¿Qué es el teorema del límite central?
El teorema del límite central es un principio en estadística que establece que, dado un tamaño de muestra suficientemente grande, la distribución de la media de estas muestras se aproxima a una distribución normal, independientemente de la forma de la distribución poblacional original. Este teorema es crucial para realizar inferencias sobre poblaciones basadas en muestras.
¿Por qué es importante el teorema del límite central en Excel?
El teorema del límite central es fundamental para el análisis estadístico, ya que permite a los analistas y a los investigadores hacer inferencias sobre una población a partir de datos muestrales. En Excel, puedes aplicar el TLC para realizar cálculos probabilísticos y análisis estadísticos de manera sencilla y accesible, facilitando la visualización de datos y la toma de decisiones informadas.
¿Cuáles son los límites del teorema del límite central?
Las limitaciones del teorema del límite central incluyen: (1) un tamaño de muestra pequeño puede no resultar en una aproximación normal adecuada, especialmente si la población original es altamente sesgada; y (2) el TLC asume que los datos son independientes y que la muestra es aleatoria, lo que puede no ser el caso en todas las situaciones.

Tribradaliadq: ¡Totalmente de acuerdo, Skabelha! A mí también me costó entenderlo al principio, pero cuando lo usé en un análisis de datos para un trabajo de estadística, ¡me voló la cabeza ver cómo se ajustaban las distribuciones! Es impresionante lo que puedes lograr con Excel. ¡Qué buen artículo!
Yared: ¡Me encanta lo que comentan! A mí me pasó algo similar, Skabelha. Una vez lo implementé para un análisis de encuestas y quedé alucinado al ver cómo el teorema del límite central realmente hacía que todo encajara. ¡Definitivamente es una herramienta poderosa en Excel!
Eduardo Augusto: ¡Qué bueno que todos lo hayan encontrado útil! A mí me pasó algo parecido, al principio me parecía un lío, pero un día decidí aplicarlo en un proyecto de investigación y fue como abrir un mundo nuevo. Ver cómo las muestras se comportaban según el teorema del límite central fue alucinante, ¡y todo gracias a Excel! ¡Gracias por compartir este artículo tan clarito!
Skabelha: ¡Genial artículo! La verdad es que nunca había entendido bien el teorema del límite central hasta que lo apliqué en Excel para un proyecto de clases. Me sorprendió ver cómo se comportaban las muestras, fue todo un descubrimiento. ¡Gracias por la claridad en la explicación!