¿Te has encontrado alguna vez frente a un conjunto de datos y te has preguntado si las diferencias entre dos grupos son significativas? La estadística puede parecer intimidante, pero gracias a herramientas como Excel, llevar a cabo un análisis de prueba t de dos muestras es más sencillo de lo que piensas. En este artículo, te guiaremos paso a paso por el proceso de realizar una prueba t, desmitificando conceptos y mostrándote cómo interpretar los resultados. No importa si eres un principiante en el mundo de los datos o un experto buscando optimizar tu flujo de trabajo, ¡prepárate para descubrir el poder de Excel en tus análisis estadísticos!
El análisis de datos es una herramienta esencial para las decisiones empresariales. Afortunadamente, Microsoft Excel ofrece una amplia gama de funciones y herramientas que nos permiten realizar diversos análisis estadísticos. En este artículo, aprenderás cómo realizar una prueba t de dos muestras en Excel, una técnica clave para comparar las medias de dos grupos diferentes. ¡No te lo pierdas y descubre cómo utilizar esta poderosa función en Excel para obtener resultados precisos y confiables!
A prueba t de dos muestras Se utiliza para probar si las medias de dos poblaciones son iguales o no.
Este tutorial explica cómo realizar una prueba t de dos muestras en Excel.
Cómo realizar una prueba t de dos muestras en Excel
Supongamos que los investigadores quieren saber si dos especies diferentes de plantas en un país en particular tienen la misma altura media. Como llevaría demasiado tiempo medir cada planta, deciden recolectar una muestra de 20 plantas de cada especie.
La siguiente imagen muestra la altura (en pulgadas) de cada planta en cada muestra:
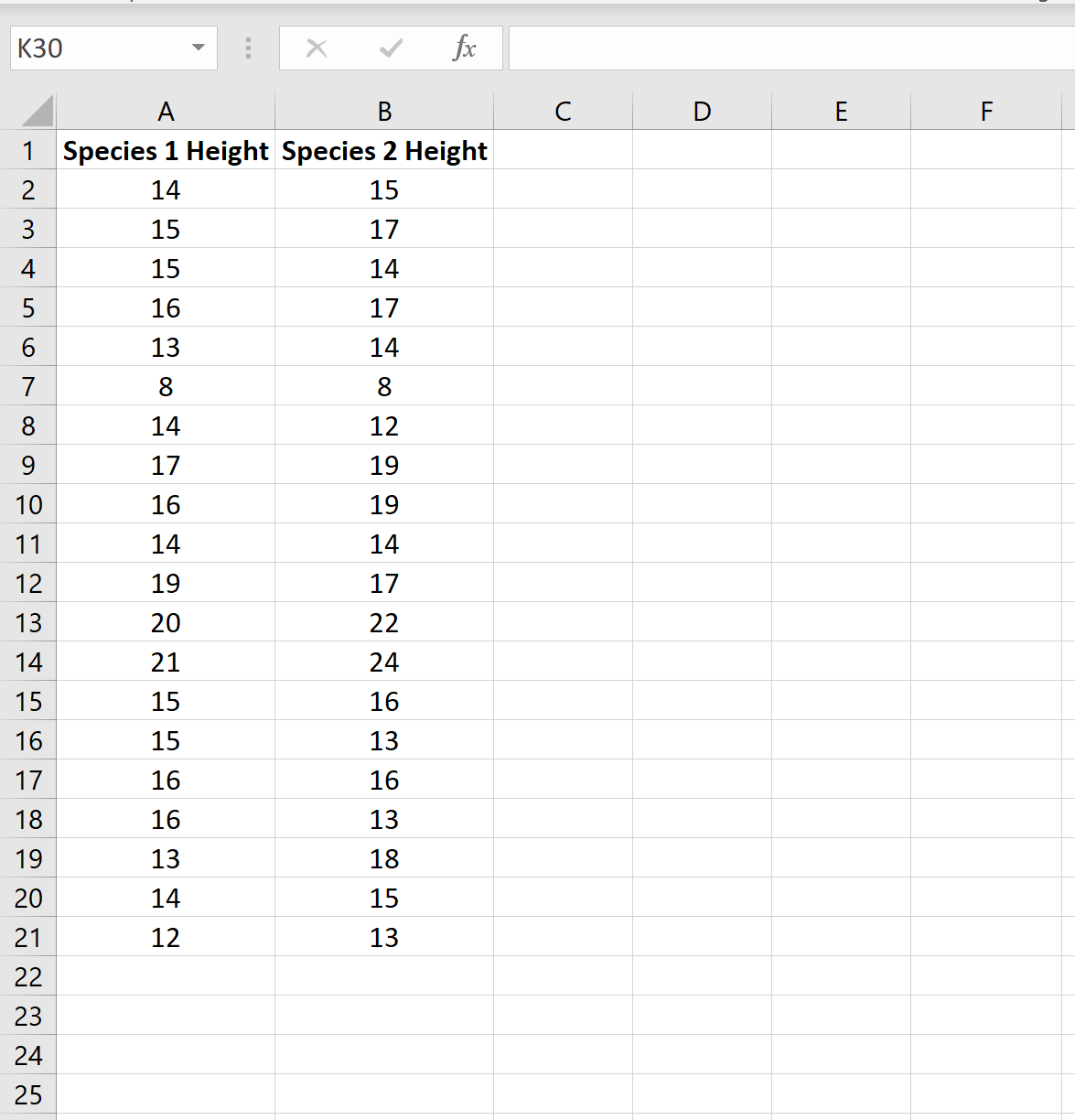
>Podemos realizar una prueba t de dos muestras para determinar si las dos especies tienen la misma altura media siguiendo los siguientes pasos:
Paso 1: determinar si las varianzas de la población son iguales.
Cuando realizamos una prueba t de dos muestras, primero debemos decidir si asumiremos que las dos poblaciones tienen varianzas iguales o desiguales. Como regla general, podemos suponer que las poblaciones tienen varianzas iguales si la relación entre la varianza de la muestra más grande y la varianza de la muestra más pequeña es menor que 4:1.
Podemos encontrar la varianza para cada muestra usando la función de Excel. =VAR.S(Rango de celdas)como muestra la siguiente imagen:
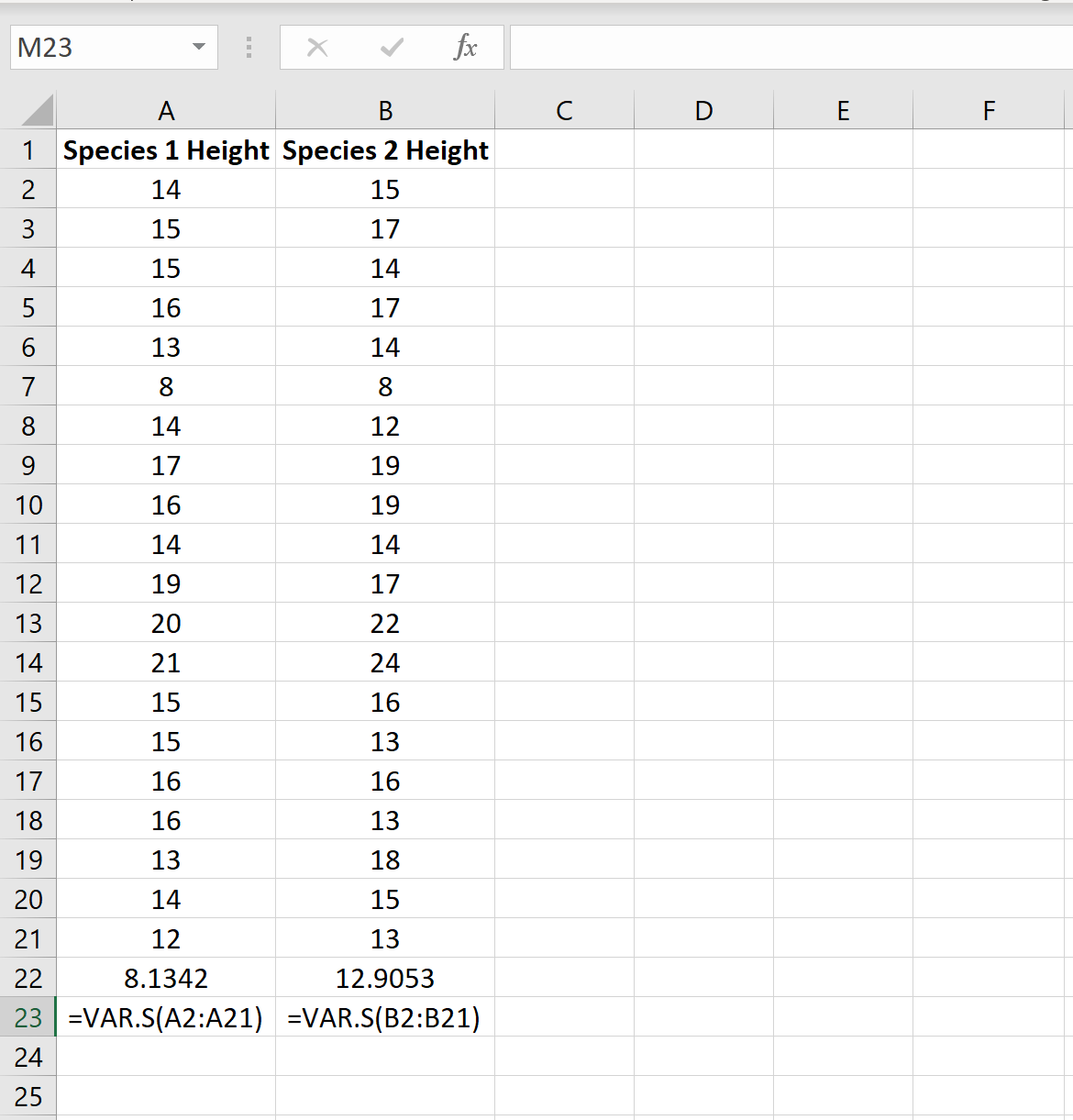
>La relación entre la varianza muestral más grande y la varianza muestral más pequeña es 12,9053 / 8,1342 = 1.586que es menor que 4. Esto significa que podemos suponer que las varianzas de la población son iguales.
Paso 2: abra el paquete de herramientas de análisis.
En la pestaña Datos en la cinta superior, haga clic en «Análisis de datos».
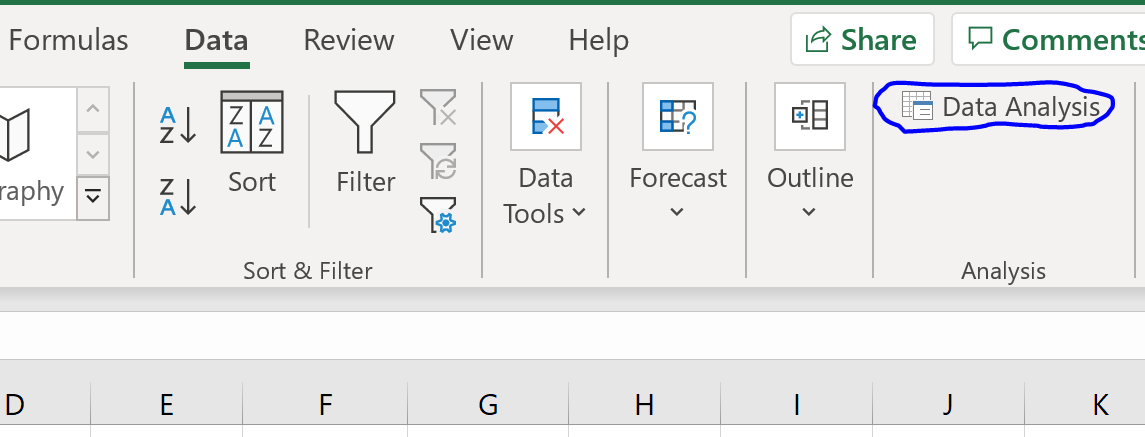
>Si no ve esto como una opción en la que hacer clic, primero debe descargar el paquete de herramientas de análisis, que es completamente gratuito.
Paso 3: seleccione la prueba adecuada a utilizar.
Selecciona la opción que dice Prueba t: dos muestras asumiendo varianzas iguales y luego haga clic en Aceptar.
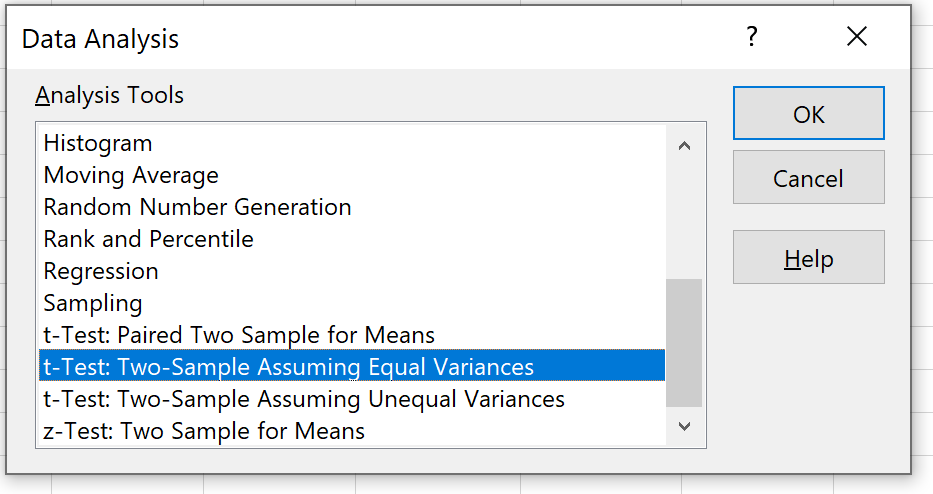
>Paso 4: Ingresa la información necesaria.
Ingrese el rango de valores para la Variable 1 (nuestra primera muestra), la Variable 2 (nuestra segunda muestra), la diferencia de medias hipotética (en este caso ponemos «0» porque queremos saber si la verdadera diferencia media de la población es 0), y el rango de salida donde nos gustaría ver los resultados de la prueba t. Luego, haga clic en Aceptar.
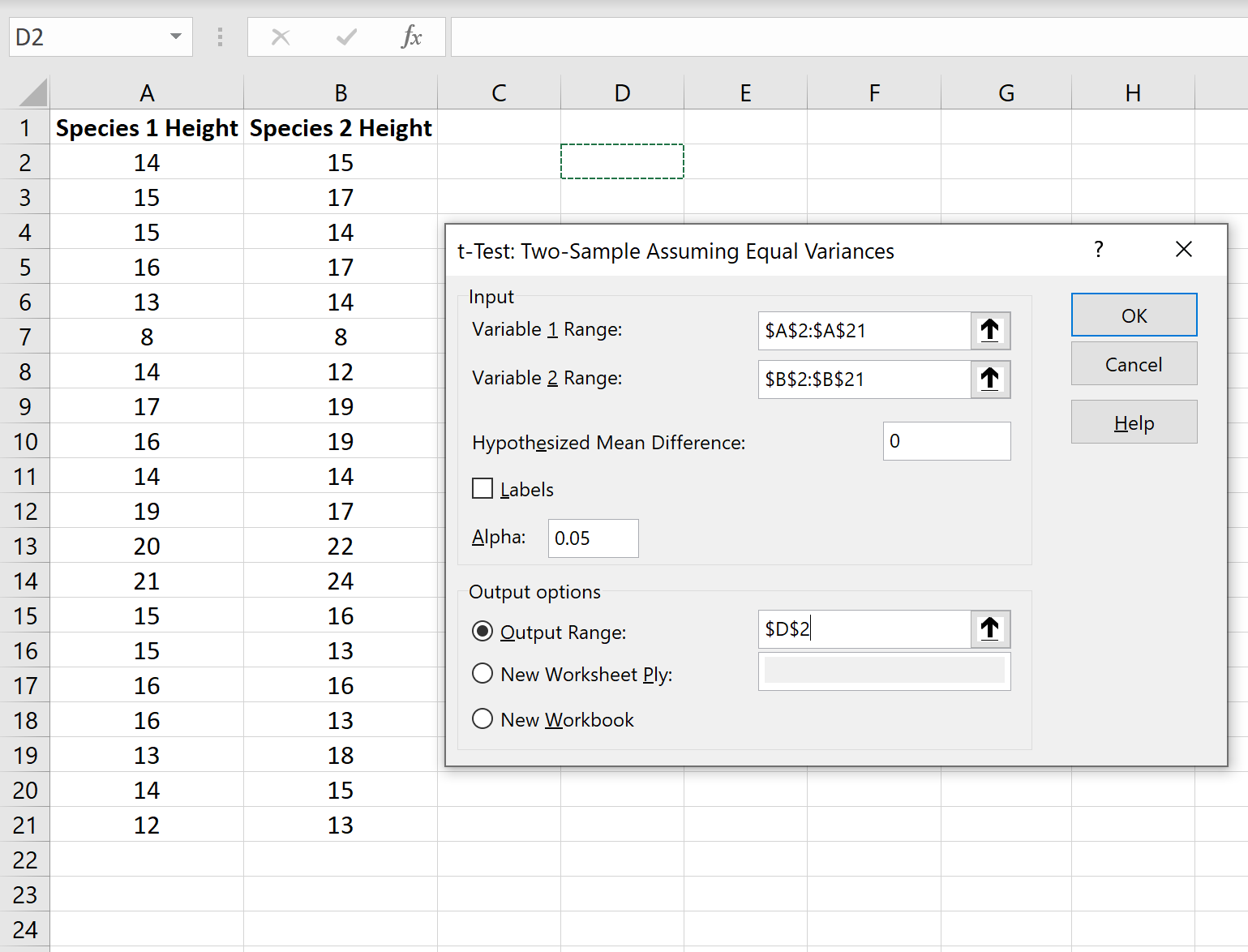
>Paso 5: interpretar los resultados.
Una vez que haga clic en Aceptar en el paso anterior, se mostrarán los resultados de la prueba t.
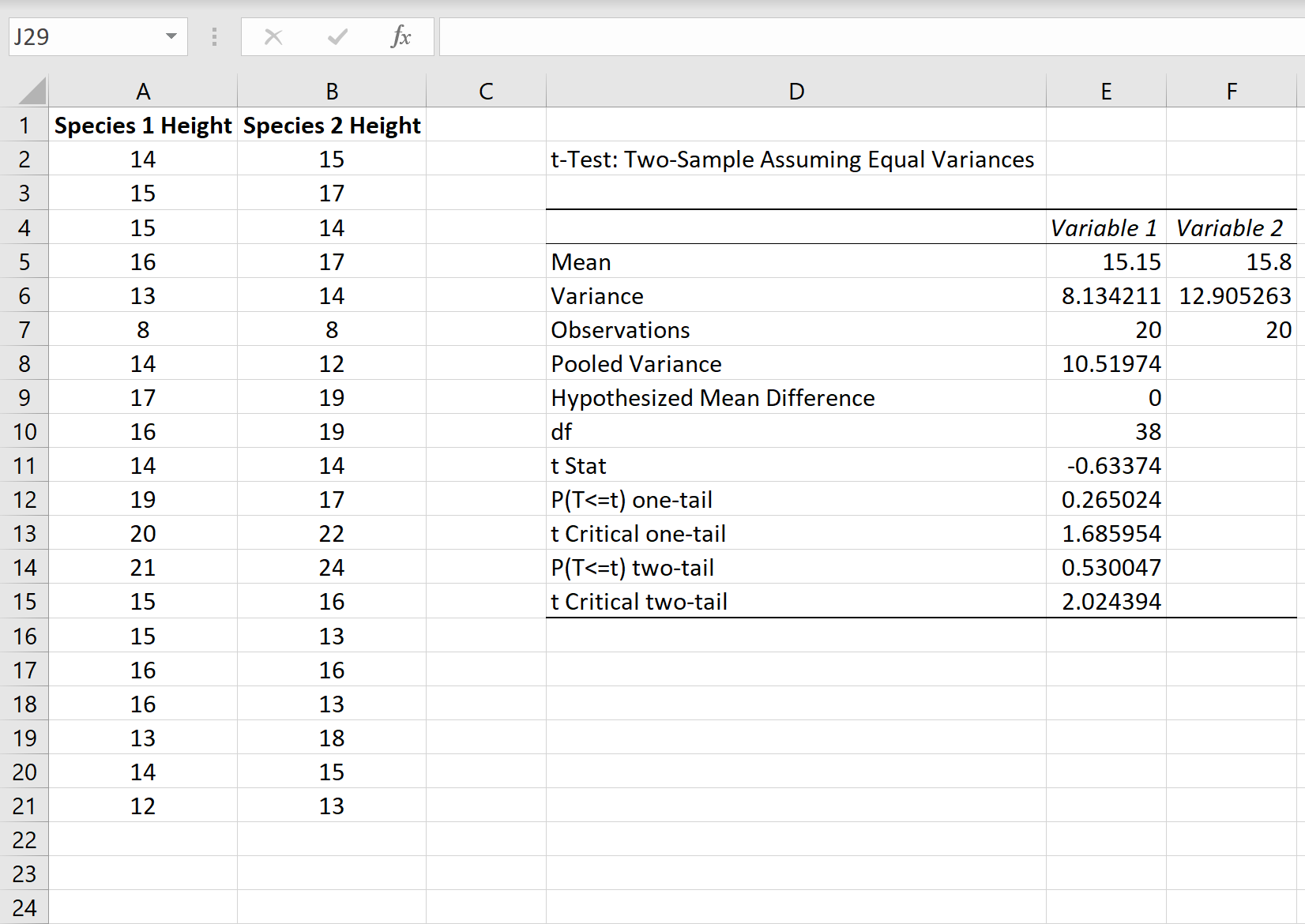
>A continuación se explica cómo interpretar los resultados:
Significar: Esta es la media para cada muestra. La muestra 1 tiene una altura media de 15.15 y la muestra 2 tiene una altura media de 15.8.
Diferencia: Esta es la varianza de cada muestra. La muestra 1 tiene una variación de 8.13 y la muestra 2 tiene una varianza de 12.90.
Observaciones: Este es el número de observaciones en cada muestra. Ambas muestras tienen 20 observaciones (por ejemplo, 20 plantas individuales en cada muestra).
Variación agrupada: Un número que se calcula “agrupando” las varianzas de cada muestra usando la fórmula s2pag = [ (n1-1)s21 + (n2-1)s22 ] / (n.1+n2-2), que resulta ser 10.51974. Este número se utiliza posteriormente al calcular la estadística de prueba. t.
Diferencia de medias hipotética: El número que “planteamos como hipótesis” es la diferencia entre las dos medias poblacionales. En este caso elegimos 0 porque queremos probar si la diferencia entre las medias de las dos poblaciones es 0, por ejemplo, no hay diferencia.
df: Los grados de libertad para la prueba t, calculados como n1 + norte2 -2 = 20 + 20 – 2 = 38.
t Estadísticas: La estadística de prueba tcalculado como t = [ x1 – x2 ] / √ [ s2p(1/n1 + 1/n2) ]
En este caso, t = [15.15-15.8] / √ [ 10.51974(1/20+1/20) ] = -0.63374.
P(T<=t) de dos colas: El valor p para una prueba t de dos colas. En este caso p = 0.530047. Esto es mucho mayor que alfa = 0,05, por lo que no podemos rechazar la hipótesis nula. No tenemos evidencia suficiente para decir que las dos medias poblacionales sean diferentes.
t Crítico de dos colas: Este es el valor crítico de la prueba, que se encuentra identificando el valor en la tabla de distribución t que corresponde a una prueba de dos colas con alfa = 0,05 y df = 38. Esto resulta ser 2.024394. Desde nuestra estadística de prueba t es menor que este valor, no podemos rechazar la hipótesis nula. No tenemos evidencia suficiente para decir que las dos medias poblacionales sean diferentes.
Tenga en cuenta que el enfoque del valor p y del valor crítico conducirán a la misma conclusión.
Recursos adicionales
Los siguientes tutoriales explican cómo realizar otros tipos de pruebas t en Excel:
Cómo realizar una prueba t de una muestra en Excel
Cómo realizar una prueba t de muestras pareadas en Excel
Cómo realizar una prueba t de dos muestras en Excel – Preguntas frecuentes
Cómo se realiza una prueba t de dos muestras en Excel
Realizar una prueba t de dos muestras en Excel es una forma útil de comparar las medias de dos grupos para determinar si existen diferencias significativas entre ellos. A continuación, te presentamos algunas preguntas frecuentes relacionadas con la realización de este tipo de pruebas en Excel.
¿Qué es una prueba t de dos muestras?
Una prueba t de dos muestras es un método estadístico utilizado para comparar las medias de dos grupos independientes y determinar si las diferencias observadas son estadísticamente significativas. Esta prueba se basa en la distribución t de Student y es ampliamente utilizada en estudios de investigación y análisis de datos.
¿Cuándo debería usar una prueba t de dos muestras en Excel?
Deberías utilizar una prueba t de dos muestras en Excel cuando tengas dos grupos independientes y desees evaluar si hay una diferencia significativa entre sus medias. Por ejemplo, puedes usar esta prueba para comparar las calificaciones de dos grupos de estudiantes expuestos a diferentes métodos de enseñanza y determinar si uno es más efectivo que el otro.
¿Cómo se realiza una prueba t de dos muestras en Excel?
Realizar una prueba t de dos muestras en Excel es relativamente sencillo si sigues estos pasos:
Encontrarás más información detallada sobre cómo realizar una prueba t de dos muestras en Excel en la documentación de Microsoft.
¿Cuál es la interpretación de los resultados de una prueba t de dos muestras?
La interpretación de los resultados de una prueba t de dos muestras depende del valor obtenido y del nivel de significancia establecido. Si el valor de la prueba es menor que el nivel de significancia (generalmente 0,05), se puede concluir que existen diferencias estadísticamente significativas entre las medias de los grupos. De lo contrario, no se pueden considerar diferencias significativas.
Recuerda que una prueba t de dos muestras en Excel solo proporciona información sobre la probabilidad de las diferencias observadas. Es importante tener en cuenta otros factores y consideraciones relevantes para obtener conclusiones adecuadas en tu análisis.
Conclusiones
La prueba t de dos muestras en Excel es una herramienta poderosa para comparar las medias de dos grupos y determinar si las diferencias encontradas son estadísticamente significativas. Conocer cómo realizar esta prueba y su correcta interpretación puede ayudarte a tomar decisiones basadas en evidencia y respaldadas por datos consistentes.
Si deseas aprender más sobre el análisis estadístico en Excel, te recomendamos explorar los recursos ofrecidos por la página oficial de soporte de Microsoft para Excel o buscar material adicional en fuentes confiables.
[automatic_youtube_gallery type=»search» search=»Cómo realizar una prueba t de dos muestras en Excel» limit=»1″]
Cómo realizar una prueba t de dos muestras en Excel
¿Te has encontrado alguna vez frente a un conjunto de datos y te has preguntado si las diferencias entre dos grupos son significativas? La estadística puede parecer intimidante, pero gracias a herramientas como Excel, llevar a cabo un análisis de prueba t de dos muestras es más sencillo de lo que piensas. En este artículo, te guiaremos paso a paso por el proceso de realizar una prueba t, desmitificando conceptos y mostrándote cómo interpretar los resultados.
¿Qué es una prueba t de dos muestras?
Una prueba t de dos muestras es un método estadístico utilizado para comparar las medias de dos grupos independientes y determinar si las diferencias observadas son estadísticamente significativas. Esta prueba se basa en la distribución t de Student y es ampliamente utilizada en estudios de investigación y análisis de datos.
¿Cuándo utilizar una prueba t de dos muestras en Excel?
Deberías utilizar esta prueba cuando tengas dos grupos independientes y desees evaluar si hay una diferencia significativa entre sus medias. Por ejemplo, puedes usar esta prueba para comparar las calificaciones de dos grupos de estudiantes expuestos a diferentes métodos de enseñanza y determinar si uno es más efectivo que el otro.
Pasos para realizar una prueba t de dos muestras en Excel
- Determinar si las varianzas son iguales: Antes de realizar la prueba, verifica si las varianzas de las poblaciones son iguales. Una regla general es que si la relación entre la varianza de la muestra más grande y la varianza de la muestra más pequeña es menor que 4:1, puedes asumir que son iguales.
- Abrir el paquete de herramientas de análisis: Ve a la pestaña Datos en la cinta superior y haz clic en Análisis de datos. Si no lo ves, primero debes descargar el paquete de herramientas de análisis, que es gratuito.
- Seleccionar la prueba adecuada: Escoge la opción que dice Prueba t: dos muestras asumiendo varianzas iguales y haz clic en Aceptar.
- Ingresar la información necesaria: Introduce el rango de valores para la primera y segunda muestra, la diferencia hipotética de medias (generalmente 0) y el rango de salida donde deseas ver los resultados.
- Interpretar los resultados: Examina las estadísticas de la prueba t, incluyendo la media para cada muestra, la diferencia, la varianza, los grados de libertad, y el valor p, entre otros.
Interpretación de los resultados
Una vez que realices la prueba, recibirás un informe con varios resultados clave:
- Media: Indica la media de cada muestra.
- Diferencia de medias hipotética: Este es el número que planteas como hipótesis, generalmente se establece en 0.
- Valor p: Un valor p alto indica que no hay diferencias significativas entre las medias de las dos poblaciones, mientras que un valor p bajo sugiere que sí las hay.
Recursos adicionales
Si deseas profundizar más en el análisis estadístico con Excel, te recomendamos los siguientes artículos:
- Cómo realizar una prueba t de una muestra en Excel
- Cómo realizar una prueba t de muestras pareadas en Excel
Preguntas Frecuentes (FAQs)
¿Qué es una prueba t de dos muestras?
Una prueba t de dos muestras es un método estadístico utilizado para comparar las medias de dos grupos independientes y determinar si las diferencias observadas son estadísticamente significativas. Esta prueba se basa en la distribución t de Student y es ampliamente utilizada en estudios de investigación y análisis de datos.
¿Cómo se realiza una prueba t de dos muestras en Excel?
Realizar una prueba t de dos muestras en Excel es relativamente sencillo. Debes asegurarte de tener tus datos organizados en columnas y seguir los pasos mencionados anteriormente. Excel te proporcionará un resumen detallado de los resultados que podrás interpretar fácilmente.
¿Cuál es la importancia del valor p en una prueba t?
El valor p es crucial en la prueba t, ya que determina si debes rechazar la hipótesis nula. Un valor p menor que el nivel de significancia (comúnmente 0.05) sugiere que hay diferencias significativas entre las medias de los dos grupos, mientras que un valor p mayor sugiere lo contrario.
¿Qué hacer si las varianzas son desiguales?
Si determinas que las varianzas son desiguales, debes seleccionar la opción de Prueba t: dos muestras asumiendo varianzas desiguales en el paquete de herramientas de análisis de Excel para obtener resultados más precisos.
Cham: ¡Sí, totalmente! A mí también me ayudó un montón, sobre todo cuando tuve que hacer una prueba t para mi tesis, y pensé que iba a darme dolores de cabeza. Pero con lo que explicas aquí, todo fluyó. ¡Gran trabajo!
AdagadAnoniG: ¡Me encantó el artículo! La prueba t puede parecer complicada, pero con las explicaciones que diste, se hace mucho más fácil. Recientemente, tuve que compararlo en un proyecto de investigación y, gracias a tus pasos, me sentí mucho más seguro al usar Excel. ¡Gracias por compartir estos tips!
Juan ildefonso: ¡Qué buen artículo! La verdad es que la prueba t siempre me había parecido un lío, pero con tus explicaciones, todo se aclaró. Justo la usé para un análisis en un curso de estadística hace poco, y me sentí mucho más tranquilo al manejar Excel. ¡Mil gracias por hacer esto tan accesible!
Baraja: ¡Oh, me alegra leer sus comentarios! La verdad es que la prueba t me intimidaba bastante antes, pero una vez que le agarro la onda, me di cuenta de lo útil que es. En un proyecto en la universidad, tuve que aplicar esta prueba y, gracias a lo que aprendí, logré presentar mis resultados sin estrés. Así que mil gracias por este artículo tan claro, definitivamente me ayudó a ganar confianza. ¡Sigan así!