¿Te has preguntado alguna vez cómo analizar datos no paramétricos de manera efectiva? La prueba de Friedman es una herramienta poderosa que te permite comparar tres o más grupos relacionados, y lo mejor de todo es que puedes realizarla fácilmente en Excel. En este artículo, te guiaré paso a paso a través del proceso para que puedas aplicar esta prueba en tus propios análisis. Descubre cómo Excel puede convertirse en tu aliado ideal para desentrañar patrones y tomar decisiones más informadas. ¡Vamos a ello!
La prueba de Friedman es una herramienta estadística fundamental para analizar datos relacionados con varias variables independientes. Si eres usuario de Excel y te interesa aprender cómo realizar esta prueba, estás en el lugar correcto. En este artículo, te guiaré paso a paso a través del proceso de realizar la prueba de Friedman en Excel, y te proporcionaré todos los conocimientos necesarios para que puedas sacar el máximo provecho de esta valiosa técnica de análisis de datos. ¡Sigue leyendo para descubrir cómo puedes utilizar Excel para realizar la prueba de Friedman y obtener información importante sobre tus datos!
El Prueba de Friedman es una alternativa no paramétrica al ANOVA de medidas repetidas. Se utiliza para determinar si existe o no una diferencia estadísticamente significativa entre las medias de tres o más grupos en los que aparecen los mismos sujetos en cada grupo.
Este tutorial explica cómo realizar la prueba de Friedman en Excel.
Ejemplo: la prueba de Friedman en Excel
Utilice los siguientes pasos para realizar la prueba de Friedman en Excel.
Paso 1: Ingresa los datos.
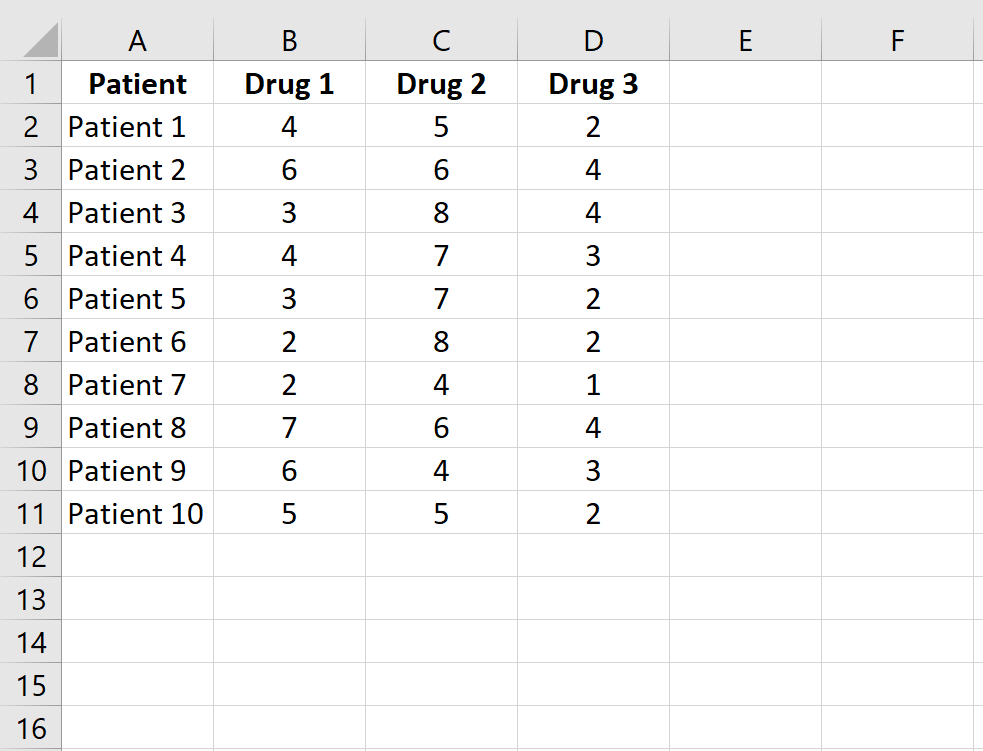
Ingrese los siguientes datos, que muestran el tiempo de reacción (en segundos) de 10 pacientes con tres medicamentos diferentes. Dado que a cada paciente se le mide cada uno de los tres medicamentos, utilizaremos la prueba de Friedman para determinar si el tiempo medio de reacción difiere entre los medicamentos.
>Paso 2: Clasificar los datos.
A continuación, clasifique los valores de datos en cada fila en orden ascendente usando el =RANGO.PROMEDIO() función. La siguiente fórmula muestra cómo calcular el rango del tiempo de respuesta del paciente 1 al medicamento 1:
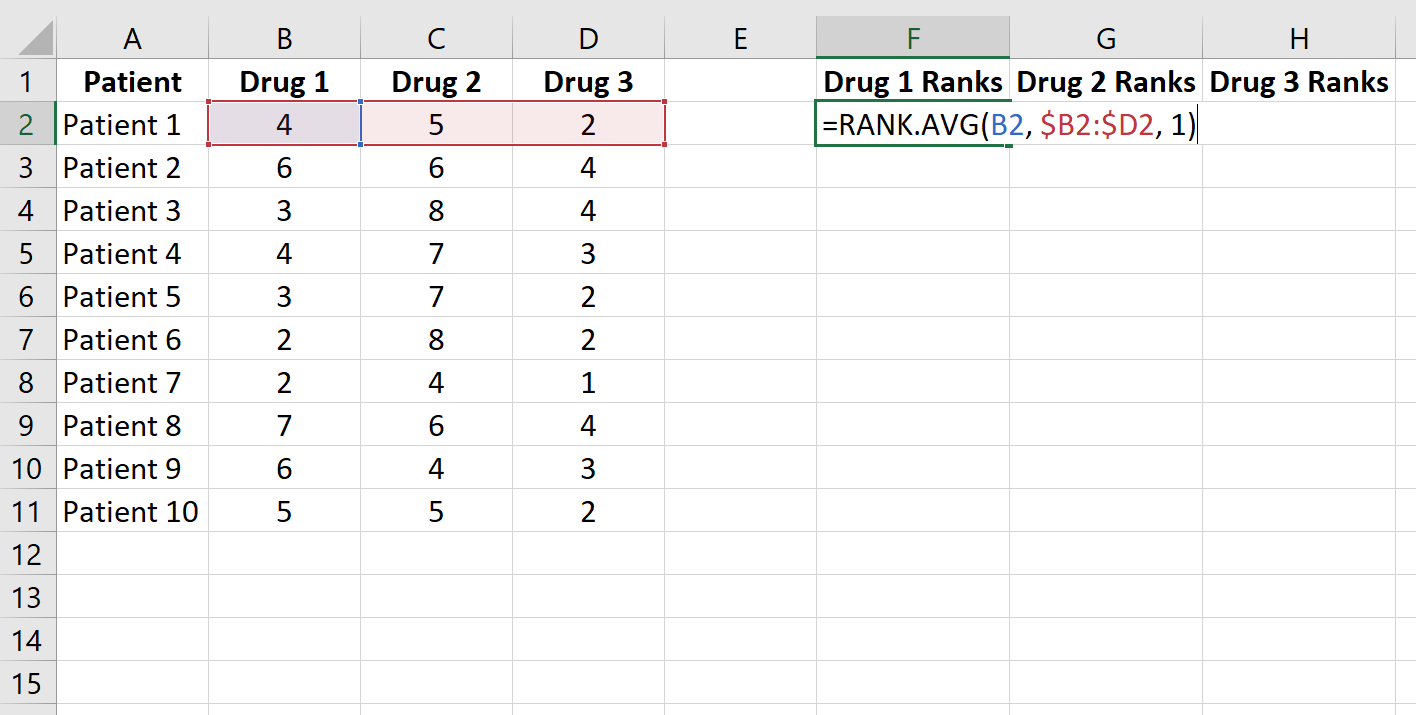
>Copie esta fórmula al resto de las celdas:
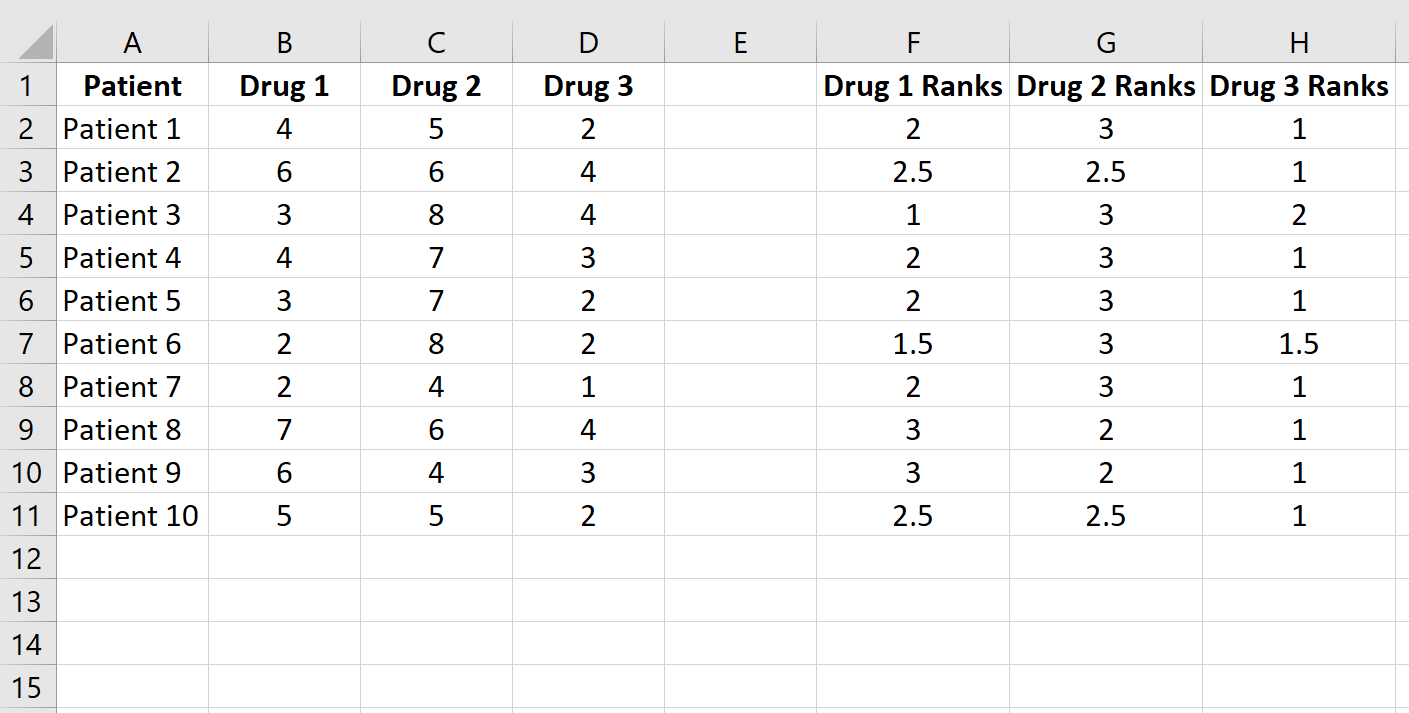
>Luego, calcule la suma de los rangos para cada columna junto con la suma de los rangos al cuadrado:
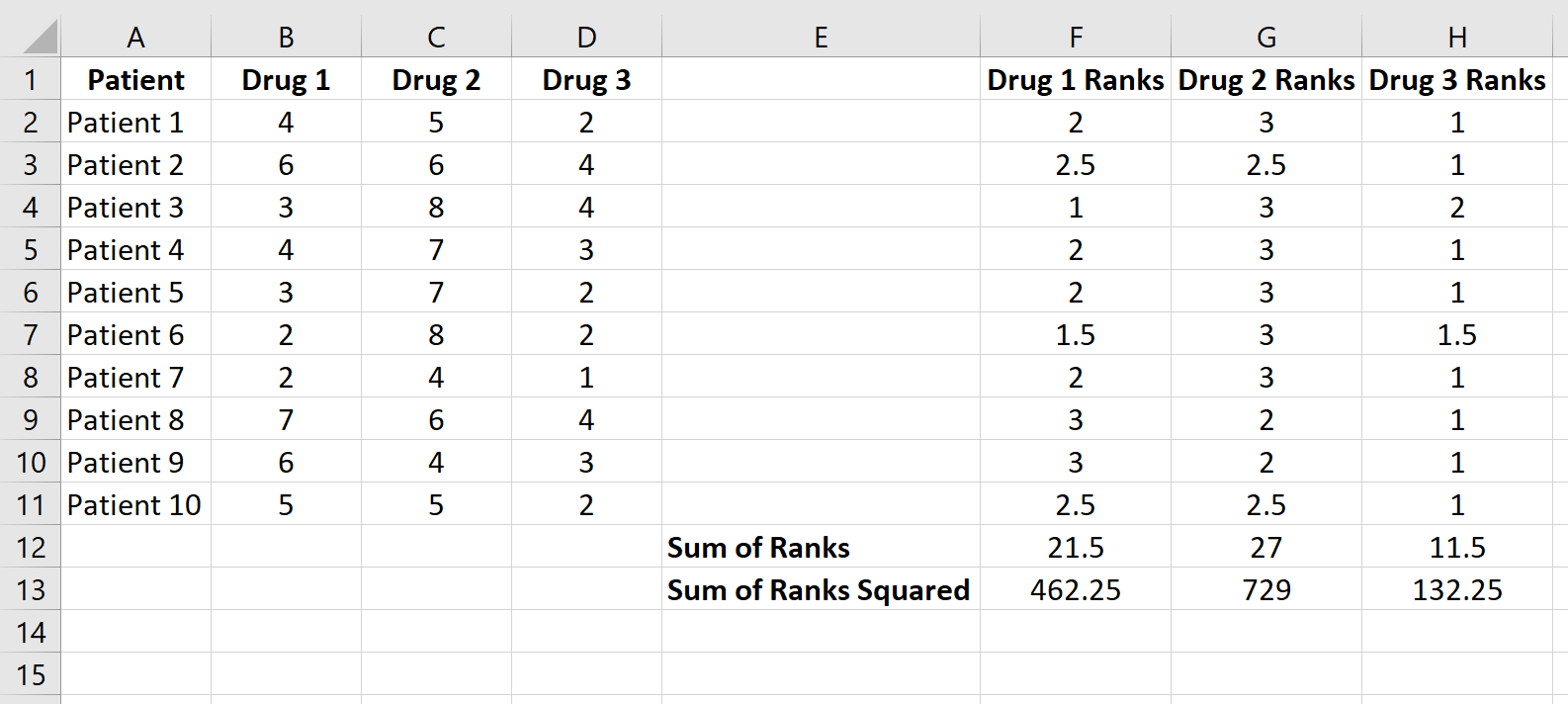
>Paso 3: Calcule el estadístico de prueba y el valor p correspondiente.
El estadístico de prueba se define como:
Q = 12/nk(k+1) * ΣRj2 – 3norte(k+1)
dónde:
- n = número de pacientes
- k = número de grupos de tratamiento
- Rj2 = suma de rangos para jth grupo
Bajo la hipótesis nula, Q sigue una distribución chi-cuadrado con k-1 grados de libertad.
La siguiente captura de pantalla muestra las fórmulas utilizadas para calcular el estadístico de prueba, Q, y el valor p correspondiente:
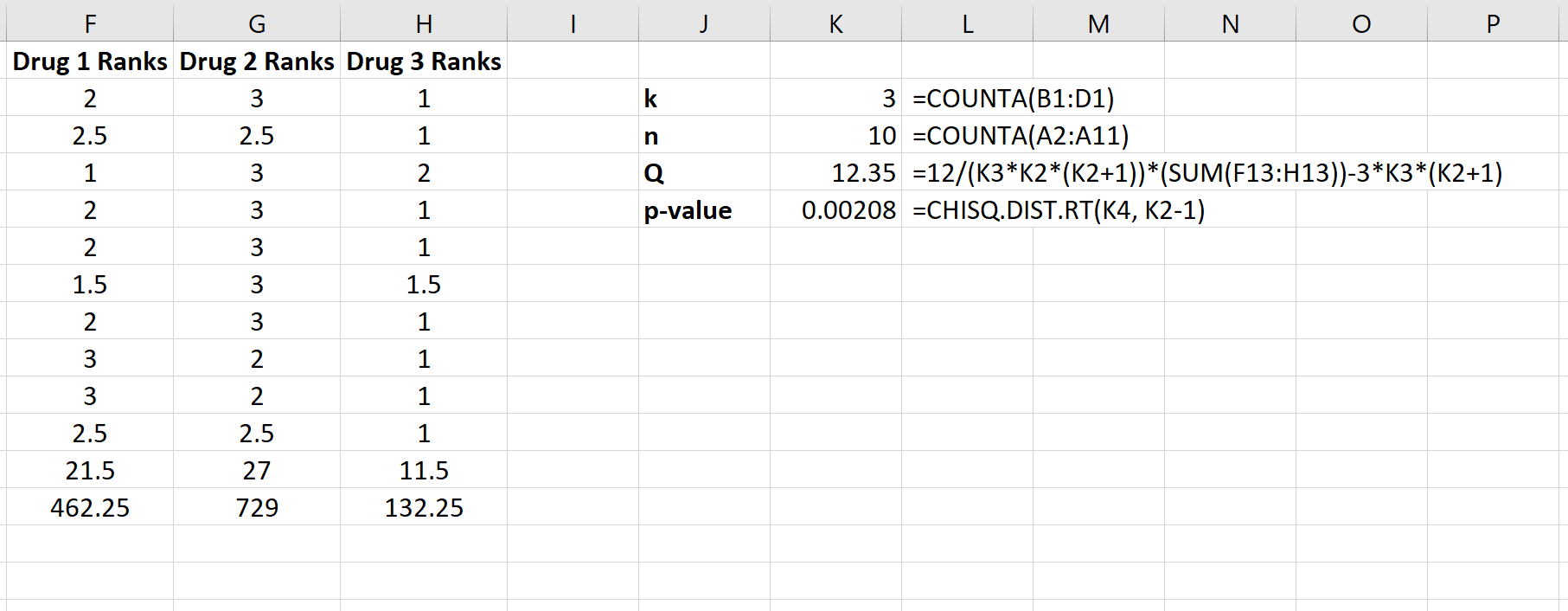
>El estadístico de prueba es Q = 12.35 y el valor p correspondiente es p = 0.00208. Dado que este valor es inferior a 0,05, podemos rechazar la hipótesis nula de que el tiempo medio de respuesta es el mismo para los tres fármacos. Disponemos de evidencia suficiente para concluir que el tipo de fármaco utilizado produce diferencias estadísticamente significativas en el tiempo de respuesta.
Paso 4: Informe los resultados.
Por último, queremos informar los resultados de la prueba. A continuación se muestra un ejemplo de cómo hacerlo:
Se realizó una prueba de Friedman en 10 pacientes para examinar el efecto que tenían tres fármacos diferentes en el tiempo de respuesta. Cada paciente usó cada medicamento una vez.
Los resultados mostraron que el tipo de fármaco utilizado condujo a diferencias estadísticamente significativas en el tiempo de respuesta (Q = 12,35, p = 0,00208).
Friedman Example 1 in Excel
Preguntas frecuentes sobre cómo realizar la prueba de Friedman en Excel
Preguntas frecuentes sobre cómo realizar la prueba de Friedman en Excel
¿Qué es la prueba de Friedman?
La prueba de Friedman es una prueba no paramétrica utilizada para comparar múltiples muestras relacionadas. Esta prueba determina si existen diferencias significativas entre los grupos o muestras seleccionados. En este caso, la prueba se realiza utilizando Microsoft Excel como herramienta.
¿Cuáles son los requisitos para realizar la prueba de Friedman en Excel?
Para poder realizar la prueba de Friedman en Excel, se requiere tener acceso a una versión de Microsoft Excel que incluya la opción «Análisis de datos». Esta opción se puede encontrar en la pestaña «Datos» del menú principal de Excel.
¿Cómo se realiza la prueba de Friedman en Excel?
Para realizar la prueba de Friedman en Excel, sigue estos pasos:
¿Qué nos proporciona la prueba de Friedman en Excel?
La prueba de Friedman en Excel nos proporciona un valor de prueba (estadística de prueba) y un valor p. El valor de prueba nos ayuda a determinar si existen diferencias significativas entre los grupos o muestras, mientras que el valor p nos permite evaluar la significancia estadística de los resultados.
¿Cómo interpretar los resultados de la prueba de Friedman en Excel?
Para interpretar los resultados de la prueba de Friedman en Excel, debemos prestar atención al valor p calculado. Si el valor p es menor o igual a un nivel de significancia predefinido (generalmente 0.05), podemos concluir que existen diferencias significativas entre los grupos o muestras analizadas. En caso contrario, no podemos rechazar la hipótesis nula y asumimos que no hay diferencias significativas.
Referencias externas:
A continuación, te proporcionamos algunos enlaces útiles para obtener más información sobre cómo realizar la prueba de Friedman en Excel:
[automatic_youtube_gallery type=»search» search=»Cómo realizar la prueba de Friedman en Excel» limit=»1″]
Cómo realizar la prueba de Friedman en Excel
¿Te has preguntado alguna vez cómo analizar datos no paramétricos de manera efectiva? La prueba de Friedman es una herramienta poderosa que te permite comparar tres o más grupos relacionados. Además, puedes realizarla fácilmente en Excel. En este artículo, te guiaré paso a paso a través del proceso para que puedas aplicar esta prueba en tus propios análisis.
¿Qué es la prueba de Friedman?
La prueba de Friedman es una prueba no paramétrica que se utiliza para comparar múltiples muestras relacionadas. Es la alternativa no paramétrica al ANOVA de medidas repetidas y permite determinar si existen diferencias significativas entre las medias de tres o más grupos en los que aparecen los mismos sujetos en cada grupo.
Requisitos para realizar la prueba en Excel
Para poder realizar la prueba de Friedman en Excel, necesitarás:
- Acceso a una versión de Microsoft Excel que incluya la opción de «Análisis de datos».
- Un conjunto de datos donde los sujetos se midan en tres o más condiciones o tratamientos.
Pasos para realizar la prueba de Friedman en Excel
A continuación te muestro los pasos que debes seguir:
Paso 1: Ingresa los datos
Ingresa tus datos en Excel, asegurándote de que cada fila corresponda a un sujeto y cada columna a un tratamiento. Por ejemplo, considera el tiempo de reacción (en segundos) de 10 pacientes con tres medicamentos diferentes.
Paso 2: Clasificar los datos
Clasifica los valores de datos en cada fila en orden ascendente usando la función =RANGO.PROMEDIO(). Esto te permitirá analizar los rangos de cada medicamento para cada paciente.
Paso 3: Calcular el estadístico de prueba y el valor p
El estadístico de prueba Q se define como:
Q = 12/nk(k+1) * ΣRj² – 3n(k+1)
Donde:
- n = número de pacientes
- k = número de grupos de tratamiento
- Rj² = suma de rangos para el j-ésimo grupo
En Excel, puedes usar fórmulas para calcular este estadístico y el valor p correspondiente. Recuerda verificar que el valor p sea menor que 0.05 para poder rechazar la hipótesis nula.
Paso 4: Informe los resultados
Es importante informar los resultados de la prueba. Un ejemplo sería:
“Se realizó una prueba de Friedman en 10 pacientes para examinar el efecto que tenían tres fármacos diferentes en el tiempo de respuesta. Los resultados mostraron que el tipo de fármaco utilizado condujo a diferencias estadísticamente significativas en el tiempo de respuesta (Q = 12,35, p = 0,00208).”
Preguntas Frecuentes (FAQs)
¿Qué es la prueba de Friedman?
La prueba de Friedman es una prueba no paramétrica utilizada para comparar múltiples muestras relacionadas. Esta prueba establece si existen diferencias significativas entre los grupos o muestras seleccionadas, y puede ser realizada fácilmente utilizando Microsoft Excel como herramienta.
¿Cuáles son los requisitos para realizar la prueba de Friedman en Excel?
Para realizar la prueba de Friedman en Excel, necesitas tener acceso a una versión de Microsoft Excel que incluya la opción «Análisis de datos», la cual se encuentra en la pestaña «Datos» del menú principal de Excel.
¿Qué tipo de datos necesito para usar la prueba de Friedman?
La prueba de Friedman requiere datos relacionados que provengan de las mismas unidades experimentales. Por ejemplo, mediciones repetidas de la misma variable en diferentes condiciones o grupos.
¿Dónde puedo encontrar más información sobre la prueba de Friedman?
Puedes consultar recursos adicionales como el artículo disponible en Statistics How To, que ofrece información detallada y ejemplos sobre esta prueba.
Conclusión
La prueba de Friedman es una herramienta eficaz para analizar datos no paramétricos en Excel. Siguiendo estos pasos, podrás realizar tus propios análisis y obtener conclusiones valiosas sobre tus datos. ¡Comienza a explorar el potencial de Excel en el análisis estadístico!

Rekelaphflatabp: ¡Totalmente de acuerdo! Al principio me costó un montón entender la prueba de Friedman, pero este artículo me ayudó mucho. Recuerdo que la primera vez que la utilicé en un proyecto escolar, estaba tan confundida que pensé que no iba a poder. Pero con estos tips, todo se volvió más claro y ahora me siento más que lista para usarla otra vez. ¡Gracias por compartirlo!
Oliver martin: ¡Totalmente de acuerdo! Este artículo es una joya. Yo recuerdo que la primera vez que fui a aplicar la prueba de Friedman, estaba lleno de dudas, pero después de leer guías como esta, me di cuenta de que no era tan complicado. Ahora la uso sin problemas en mis proyectos y me siento mucho más seguro. ¡Gracias por compartirlo!
En1nyee: ¡Me encantó el artículo! La prueba de Friedman siempre me había parecido complicada, pero gracias a tus explicaciones me animé a probarla. Recuerdo la primera vez que la usé para un proyecto en la uni, y no sabía ni por dónde empezar. Con este tutorial ahora me siento más segura para usar Excel y eso es un gran avance. ¡Gracias!
HinchiereD: ¡Súper útil el artículo! La primera vez que intenté aplicar la prueba de Friedman me volví loc@, pero gracias a tips como los de aquí, ahora hasta me parece fácil. A veces uno se siente perdido, pero con una buena guía, todo fluye mejor. ¡Gracias por compartir esta info!
Arita: ¡Qué bueno que te sirvió! A mí me pasó algo similar, la primera vez que hice la prueba de Friedman pensé que iba a fracasar, pero después de leer cosas como este artículo, ahora me siento mucho más confiada. Es increíble cómo un par de trucos pueden hacer que algo complicado sea tan accesible. ¡A seguir practicando!
Lucas ricardo: ¡Qué alegría leer esto! Yo también estaba perdido con la prueba de Friedman al principio. La primera vez que intenté usarla en un análisis de datos para mi trabajo, me sentía súper abrumado. Pero después de seguir consejos como los de este artículo, ya no es un dolor de cabeza. ¡A veces solo hace falta un poco de orientación para que todo tenga sentido!